《2025年期末考向标八年级数学上册冀教版》

1. (秦皇岛期末)如图,甲、乙、丙、丁四人手中各有一个圆形卡片,则卡片中的式子是分式的有( )


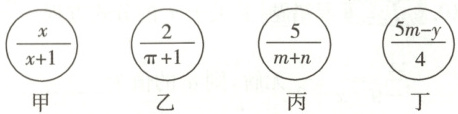
A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个

答案： 1.B

2. 若式子 $ \frac{2x - 1}{x + 5} $ 有意义,则 $ x $ 的取值范围是( )

A.$ x = \frac{1}{2} $
B.$ x = -5 $
C.$ x \neq \frac{1}{2} $
D.$ x \neq -5 $

答案： 2.D

3. (邢台期末)若 $ \frac{ab + a}{a^2} = \frac{□}{a} $,则 $ □ $ 表示( )

A.$ b + a $
B.$ ab + 1 $
C.$ b + 1 $
D.$ b $

答案： 3.C

4. (石家庄月考)计算 $ (-\frac{b}{a})^2 · a^3 = $( )

A.$ ab^2 $
B.$ -ab^2 $
C.$ \frac{b^2}{a^5} $
D.$ -\frac{b^2}{a^5} $

答案： 4.A

5. 下列分式方程中,解为 $ x = -1 $ 的是( )

A.$ \frac{4}{x - 1} = \frac{1}{x} $
B.$ \frac{x + 1}{x^2 - 1} = 0 $
C.$ \frac{2}{x - 1} + \frac{1}{x + 2} = 0 $
D.$ \frac{2}{x + 1} - \frac{1}{x + 2} = 0 $

答案： 5.C

6. 不改变分式的值,下列各式变形正确的是( )

A.$ \frac{b}{a} = \frac{b + 2}{a + 2} $
B.$ \frac{-a - b}{a + b} = -1 $
$C. \frac{a^2 - b^2}{a - b} = a - b$B
D.$ (-\frac{2x}{y})^2 = \frac{2x^2}{y^2} $

答案： 6.B

7. (石家庄期末)若 $ m $ 与 $ n $ 互为倒数,则 $ (2m - \frac{2}{n})(\frac{1}{m} + n) $ 的值为( )

A.$ 0 $
B.$ 1 $
C.$ 2 $
D.$ 3 $

答案： 7.A [解析$] \because m$与n互为倒数，$\therefore mn = 1 , \therefore (2m - \frac {2}{n}) · (\frac {1}{m} + n) = 2 + 2mn - \frac {2}{mn} - 2 = 2 + 2 - 2 - 2 = 0. $故选A.

8. 下列说法正确的是( )

A.当 $ x = 3 $ 时, $ \frac{2x + 1}{x - 3} $ 的值为 $ 0 $
B.当 $ x \neq 3 $ 时, $ \frac{x - 3}{x} $ 有意义
C.无论 $ x $ 为何值, $ \frac{5}{x + 1} $ 不可能是整数
D.无论 $ x $ 为何值, $ \frac{3}{x^2 + 1} $ 的值总为正数

答案： 8.D

9. (邯郸期中)甲、乙两组同学在植树活动中均植树 $ 120 $ 棵,已知 ______,求乙组每小时植树多少棵.下面是题目的部分解题过程,则横线上缺少的条件为( )

A.甲组每小时比乙组少植 $ 10 $ 棵,且甲组比乙组提前 $ 2 $ 小时完成
B.甲组每小时比乙组多植 $ 10 $ 棵,且乙组比甲组提前 $ 2 $ 小时完成
C.甲组每小时比乙组少植 $ 10 $ 棵,且乙组比甲组提前 $ 2 $ 小时完成
D.甲组每小时比乙组多植 $ 10 $ 棵,且甲组比乙组提前 $ 2 $ 小时完成

答案： 9.D

10. (邢台期中)已知 $ A = \frac{x^2 - 9}{x^2 + 6x + 9} ÷ \frac{x}{x + 3} $,关于甲、乙、丙的说法,下列判断正确的是( )
甲: $ A $ 的计算结果为 $ \frac{x - 3}{x} $;
乙:当 $ x = -3 $ 时, $ A = 2 $;
丙:当 $ 0 ＜ x ＜ 3 $ 时, $ A $ 的值为正数.

A.乙错,丙对
B.甲和乙都对
C.甲对,丙错
D.甲错,丙对

答案： 10.C [解析$]A = \frac {x^{2} - 9}{x^{2} + 6x + 9} ÷ \frac {x}{x + 3} = \frac {(x + 3)(x - 3)}{(x + 3)^{2}} · \frac {x + 3}{x} = \frac {x - 3}{x}，$故甲对；当x = - 3时，x + 3 = 0，分式无
意义，故乙错；当0 ＜ x ＜ 3时，x - 3 ＜ 0，$\therefore A = \frac {x - 3}{x} ＜ 0，$故丙错. 故选C.

11. (廊坊期末)已知分式 $ \frac{1}{5 - x} $ 的值为正数,写出一个符合条件的 $ x $ 的正整数值: ______.

答案： 11.4(答案不唯一)

12. (邢台期中)若 $ \frac{2(x - 1)}{3(x - 1)} = \frac{2}{3} $ 成立,则 $ x $ 的取值范围是 ______.

答案： $12.x \neq 1$

13. 若 $ x = 5 $ 是方程 $ \frac{1}{x - 2} = \frac{2}{x + a} $ 的解,则 $ a = $ ______.

答案： 13.1