《2025年伴你学单元达标测试卷八年级数学上册苏科版》

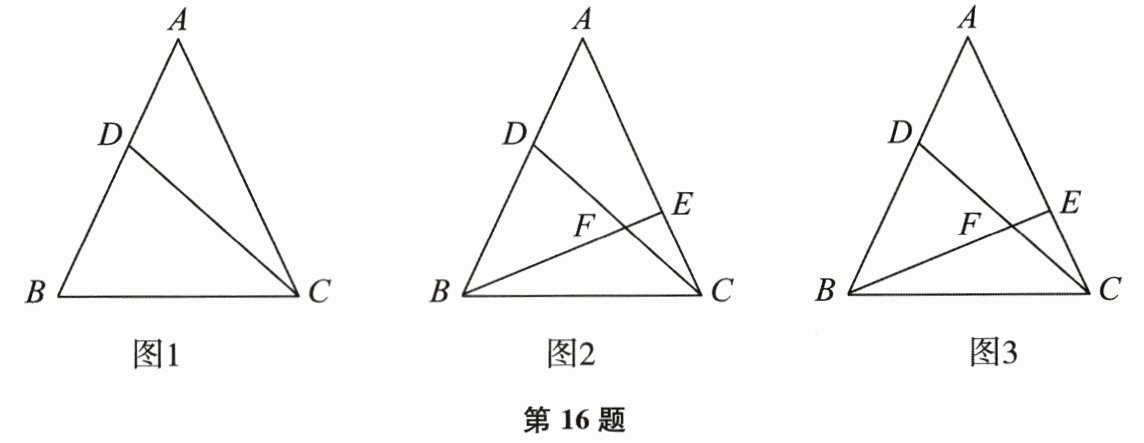
16. (本题12分)已知在 $ \triangle ABC $ 中, $ AB = AC $,点 $ D $ 是边 $ AB $ 上一点, $ \angle BCD = \angle A $.
(1) 如图1,试说明 $ CD = CB $ 的理由;
(2) 如图2,过点 $ B $ 作 $ BE \perp AC $,垂足为点 $ E $, $ BE $ 与 $ CD $ 相交于点 $ F $.
①试说明 $ \angle BCD = 2 \angle CBE $ 的理由;
②如果 $ \triangle BDF $ 是等腰三角形,求 $ \angle A $ 的度数.

答案： 16. 解：
(1)
∵AB=AC，
∴∠ABC=∠ACB，
∵∠BDC是△ADC的一个外角，
∴∠BDC=∠A+∠ACD，
∵∠ACB=∠BCD+∠ACD，∠BCD=∠A，
∴∠BDC=∠ACB，
∴CD=CB.
(2)①
∵BE⊥AC，
∴∠BEC=90°，
∴∠CBE+∠ACB=90°，
设∠CBE=α，则∠ACB=90°−α，
∴∠ACB=∠ABC=∠BDC=90°−α，
∴∠BCD=180°−∠BDC−∠ABC=180°−(90°−α)−(90°−α)=2α，
∴∠BCD=2∠CBE；
②
∵∠BFD是△CBF的一个外角，
∴∠BFD=∠CBE+∠BCD=α+2α=3α，
分三种情况：
当BD=BF时，
∴∠BDC=∠BFD=3α，
∵∠ACB=∠ABC=∠BDC=90°−α，
∴90°−α=3α，
∴α=22.5°，
∴∠A=∠BCD=2α=45°；
当DB=DF时，
∴∠DBE=∠BFD=3α，
∵∠DBE=∠ABC−∠CBE=90°−α−α=90°−2α，
∴90°−2α=3α，
∴α=18°，
∴∠A=∠BCD=2α=36°；
当FB=FD时，
∴∠DBE=∠BDF，
∵∠BDF=∠ABC＞∠DBF，
∴不存在FB=FD，
综上所述：如果△BDF是等腰三角形，∠A的度数为45°或36°.