《2025年伴你学单元达标测试卷八年级数学上册苏科版》

19. (本题12分)计算与解方程:
(1) $\sqrt{4}-\sqrt[3]{27}+\vert - 1\vert$;
(2) 解方程:$1+(x - 1)^3=-7$

答案： 19.
(1)0;　
(2)x = -1

20. (本题10分)如图.$\angle B=\angle D = 90^{\circ}$,$AB = AD$.
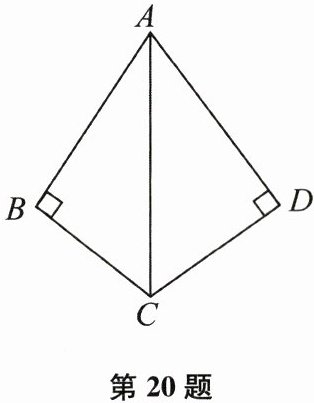
求证:$Rt\triangle ABC\congRt\triangle ADC$.

答案： 20.证明:
∵∠B = ∠D = 90°,
∴△ABC和△ADC都是直角三角形.在Rt△ABC和Rt△ADC中,$\begin{cases}AC = AC,\\AB = AD,\end{cases}$
∴Rt△ABC≌Rt△ADC(HL).