《2025年伴你学单元达标测试卷八年级数学上册苏科版》

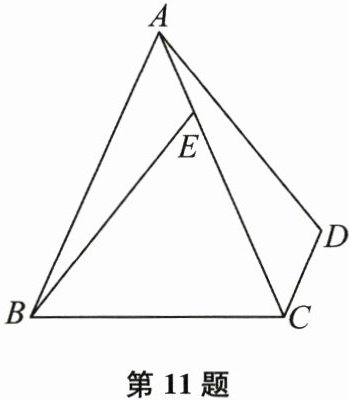
11. （本题8分）如图所示，在四边形$ABCD$中，$CD// AB$，点$E$在$AC$上，且$BE = AD$，$\angle ABE = \angle CAD$. 求证：$AE = CD$.

答案： 11.证明:
∵CD//AB,
∴∠ACD=∠BAE,
　　在△ABE和△CAD中，
　　$\begin{cases} ∠BAE=∠ACD, \\ ∠ABE=∠CAD, \\ BE=AD, \end{cases}$
∴△ABE≌△CAD(AAS),
∴AE=CD.

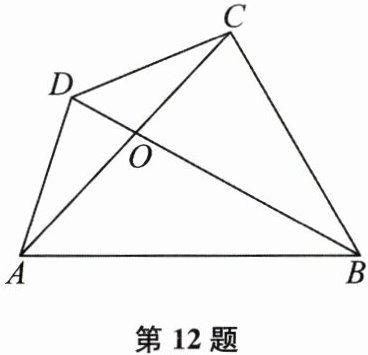
12. （本题8分）如图，在四边形$ABCD$中，$O$是$AC$与$BD$的交点，试说明：$AC$与$BD$的和小于四边形$ABCD$的周长.

答案： 12.证明:在△ABD中,AD+AB＞BD，
　　在△BCD中,CD+BC＞BD,
　　在△ACD中,AD+CD＞AC,
　　在△ABC中,AB+BC＞AC,AD+AB+CD+BC+AD+CD+AB+BC＞BD+BD+AC+AC,
∴2(AD+AB+CD+BC)＞2(AC+BD),
∴AD+AB+CD+BC＞AC+BD,
∴AC与BD的和小于四边形ABCD的周长.

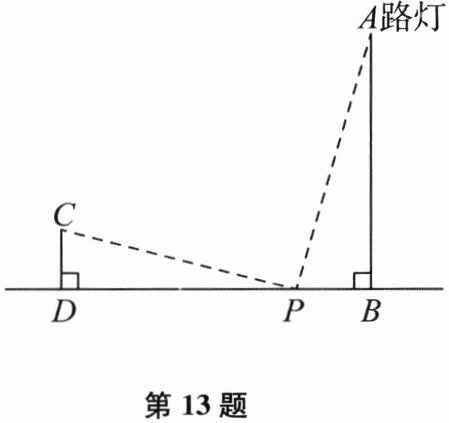
13. （本题10分）小玉利用一根长$3.6\mathrm{m}$的竿子来测量路灯$AB$的高度. 她的方法如下：如图，在路灯前选一点$P$，使$BP = 3.6\mathrm{m}$，并测得$\angle APB = 66^{\circ}$，然后把竖直的竿子$CD$（$CD = 3.6\mathrm{m}$）在$BP$的延长线上左右移动，使$\angle CPD = 24^{\circ}$，此时测得$BD = 11.6\mathrm{m}$. 请根据这些数据，计算路灯$AB$的高度.

答案： 13.解:由题意得,∠CDP=∠PBA=90°,
∵∠CPD=24°,
∴根据三角形内角和定理，∠PCD=180°−90°−24°=66°,
∵∠APB=66°，
∴∠PCD=∠APB=66°,
　　在△CPD和△PAB中，
　　$\begin{cases} ∠CDP=∠PBA=90°, \\ CD=PB=3.6, \\ ∠PCD=∠APB, \end{cases}$
∴△CPD≌△PAB(ASA),
∴PD=AB,
∵BD=11.6m,BP=3.6m,
∴AB=PD=BD−BP=11.6−3.6=8(m),
答:路灯AB的高度是8m.