《2025年伴你学单元达标测试卷八年级数学上册苏科版》

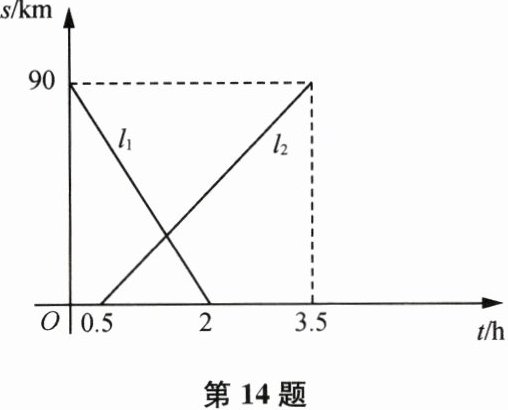
14. (本题12分)$A$、$B$两地相距$90\mathrm{km}$,甲、乙两人从两地出发相向而行,甲先出发.图中$l_{1}$,$l_{2}$表示两人离$A$地的距离$S(\mathrm{km})$与时间$t(\mathrm{h})$的关系,结合图像回答下列问题:
(1) 表示甲离$A$地的距离与时间关系的图像是l₁(填$l_{1}$或$l_{2}$);甲的速度是45$\mathrm{km/h}$;乙的速度是30$\mathrm{km/h}$.
(2) 甲出发后多少时间两人恰好相距$15\mathrm{km}$?

答案： 14.
(1)l₁,45,30。
(2)设甲对应的函数表达式为s=at + b，$\begin{cases}b = 90, \\2a + b = 0,\end{cases}$得$\begin{cases}a = - 45, \\b = 90,\end{cases}$甲对应的函数表达式为s= - 45t+90，设乙对应的函数表达式为s=ct + d，$\begin{cases}0.5c + d = 0, \\3.5c + d = 90,\end{cases}$得$\begin{cases}c = 30, \\d = - 15,\end{cases}$即对应的函数表达式为:s=30t - 15，
∴|(-45t + 90)-(30t - 15)|=15，解得,t₁=1.2,t₂=1.6，
答:甲出发后1.2h或1.6h时两人恰好相距15km。

15. (本题12分)近年来,中国传统服服饰备受大家的青睐,走上国际时装周舞台,大放异彩.某服装店直接从工厂购讲长、短两款传统服饰进行销售,进货价和销售价如表:

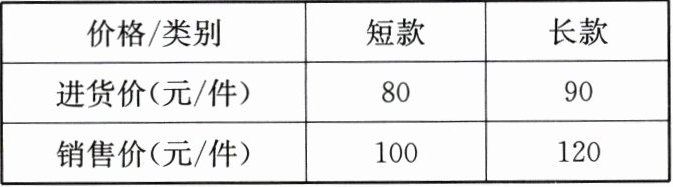
(1) 该服装店第一次用4300元购讲长、短两款服装共50件,求两款服装分别购进的件数;
(2) 第一次购进的两款服装售完后,该服装店计划再次购讲长、短两款服装共200件(进货价和销售价都不变),且第二次进货总价不高于16800元.服装店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?

答案： 15.
(1)由题意，设购进短款服装x件，购进长款服装y件，
∴$\begin{cases}x + y = 50, \\80x + 90y = 4300.\end{cases}$
∴$\begin{cases}x = 20, \\y = 30.\end{cases}$
答:短款服装购进20件，长款服装购进30件。
(2)由题意，设第二次购进m件短款服装，则购进(200 - m)件长款服装，
∴80m + 90(200 - m)≤16800。
∴m≥120。又设利润为w元，则w=(100 - 80)m + (120 - 90)(200 - m)= - 10m + 6000。
∵ - 10＜0。
∴w随m的增大而减小。
∴当m=120时，利润w最大为: - 10×120 + 6000=4800(元)。
答:当购进120件短款服装，80件长款服装时有最大利润，最大利润是4800元。