《2025年伴你学单元达标测试卷八年级数学上册苏科版》

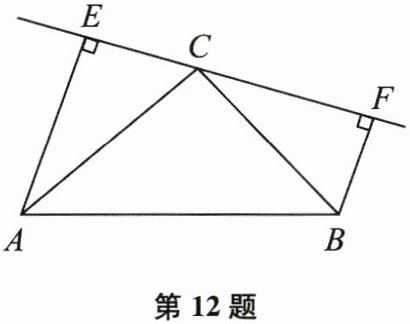
12. (本题8分)如图,在 $ \triangle ABC $ 中, $ AC = BC $,直线 $ l $ 经过顶点 $ C $,过 $ A $, $ B $ 两点分别作 $ l $ 的垂线 $ AE $, $ BF $, $ E $, $ F $ 为垂足, $ AE = CF $.求证: $ \angle ACB = 90° $.

答案： 12. 证明：如图，在Rt△ACE和Rt△CBF中，
$\begin{cases} AC=BC, \\ AE=CF, \end{cases}$
∴Rt△ACE≌Rt△CBF(HL)，
∴∠EAC=∠BCF，
∵∠EAC+∠ACE=90°，
∴∠ACE+∠BCF=90°，
∴∠ACB=180°−90°=90°.

13. (本题10分)如图,点 $ P $ 为 $ \triangle ABC $ 的内角平分线 $ BP $ 与 $ CP $ 的交点.
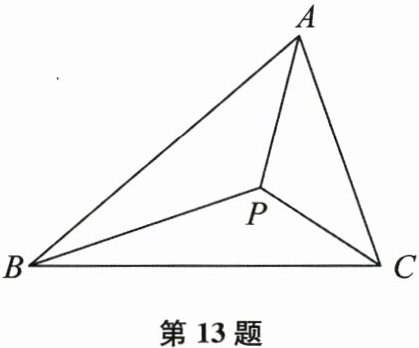
试说明: $ \angle BPC = 90° + \frac{1}{2} \angle BAC $.

答案：
13. 证明：在△ABC中，∠ABC+∠ACB+∠BAC=180°，
∴∠ABC+∠ACB=180°−∠BAC，
∵点P为△ABC的内角平分线BP与CP的交点，
∴∠PBC=$\frac{1}{2}$∠ABC，∠PCB=$\frac{1}{2}$∠ACB，
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°−∠BAC)=90°−$\frac{1}{2}$∠BAC，
∴∠BPC=180°−(90°−$\frac{1}{2}$∠BAC)=90°+$\frac{1}{2}$∠BAC.

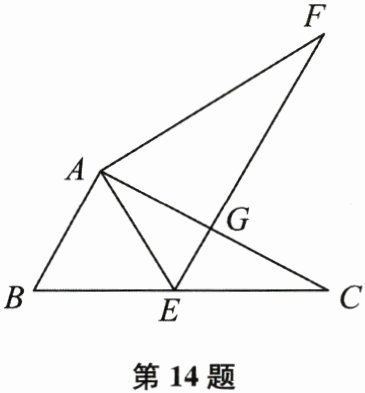
14. (本题10分)如图,在 $ \triangle ABC $ 和 $ \triangle AEF $ 中,点 $ E $ 在 $ BC $ 边上, $ AE = AB $, $ AC = AF $, $ \angle CAF = \angle BAE $, $ EF $ 与 $ AC $ 交于点 $ G $.
(1) 求证: $ EF = BC $;
(2) 若 $ \angle B = 62° $, $ \angle ACB = 24° $,求 $ \angle FGC $ 的度数.

答案： 14.
(1)证明：
∵∠CAF=∠BAE，
∴∠CAF+∠EAC=∠BAE+∠EAC，
即∠BAC=∠EAF，
在△BAC和△EAF中，
$\begin{cases} AB=AE, \\ ∠BAC=∠EAF, \\ AC=AF, \end{cases}$
∴△BAC≌△EAF(SAS)，
∴EF=BC.
(2)解：
∵AB=AE，
∴∠B=∠AEB=62°，
∴∠BAE=56°，
∴∠CAF=∠BAE=56°，
∵△BAC≌△EAF，
∴∠F=∠C=24°，
∴∠FGC=∠FAC+∠F=56°+24°=80°.

15. (本题12分)【新情境】
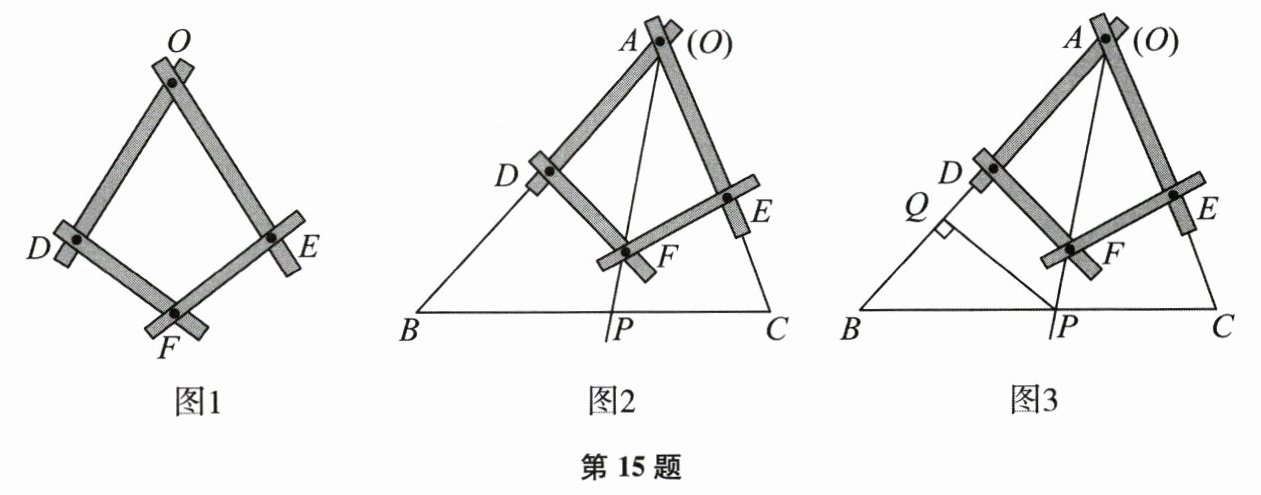
图1是一个平分角的仪器,其中 $ OD = OE $, $ FD = FE $.
(1) 如图2,将仪器放置在 $ \triangle ABC $ 上,使点 $ O $ 与顶点 $ A $ 重合, $ D $, $ E $ 分别在边 $ AB $, $ AC $ 上,沿 $ AF $ 画一条射线 $ AP $,交 $ BC $ 于点 $ P $. $ AP $ 是 $ \angle BAC $ 的平分线吗? 请判断并说明理由;
(2) 如图3,在(1)的条件下,过点 $ P $ 作 $ PQ \perp AB $ 于点 $ Q $,若 $ PQ = 4 $, $ AC = 6 $,求 $ \triangle APC $ 的面积.

答案：
15. 解：
(1)AP是∠BAC的平分线，理由如下：
在△ADF和△AEF中，
$\begin{cases} AD=AE, \\ AF=AF, \\ DF=EF, \end{cases}$
∴△ADF≌△AEF(SSS)，
∴∠DAF=∠EAF，
∴AP平分∠BAC.
(2)如图3，过点P作PM⊥AC于点M，
∵AP平分∠BAC，PQ⊥AB，
∴PM=PQ=4，
∴$S_{△APC}=\frac{1}{2}AC·PM=\frac{1}{2}×6×4=12$.