《2025年伴你学单元达标测试卷八年级数学上册苏科版》

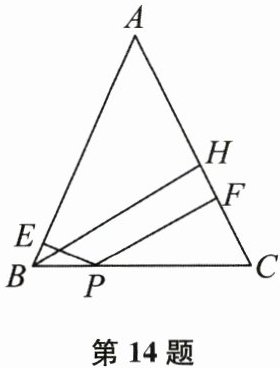
14. （本题10分）如图，$P$是等腰三角形$ABC$底边$BC$上的任一点，$PE\perp AB$于$E$，$PF\perp AC$于$F$，$BH$是等腰三角形$AC$边上的高. 试说明$PE$、$PF$和$BH$的数量关系.

答案： 14.解:连接AP.
∵AB=AC,
∴$S_{△ABC}=S_{△ABP}+S_{△ACP}=\frac{1}{2}AB×PE+\frac{1}{2}AC×PF=\frac{1}{2}AC×(PE+PF)$,
∵$S_{△ABC}=\frac{1}{2}AC×BH$,
∴PE+PF=BH.

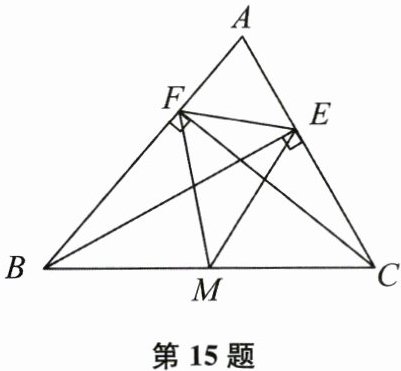
15. （本题12分）如图，在$\triangle ABC$中，$CF\perp AB$，垂足为$F$，$BE\perp AC$，垂足为$E$，$M$为$BC$的中点，连接$MF$，$ME$.
（1）求证：$ME = MF$；
（2）若$\angle ABC = 54^{\circ}$，$\angle ACB = 60^{\circ}$，求$\angle FME$的大小.

答案： 15.
(1)证明:由条件可知△BCE和△BCF均是直角三角形，又因为点M为BC的中点，
∴MF=BM=CM,ME=BM=CM,
∴ME=MF.
(2)解:
∵MB=MF,ME=MC,
∴∠MBF=∠MFB,∠MEC=∠MCE,
∵∠ABC=54°,∠ACB=60°,
∴∠BMF=180°−2×54°=72°,∠CME=180°−2×60°=60°,
∴∠EMF=180°−72°−60°=48°,
∴∠FME的度数为48°.

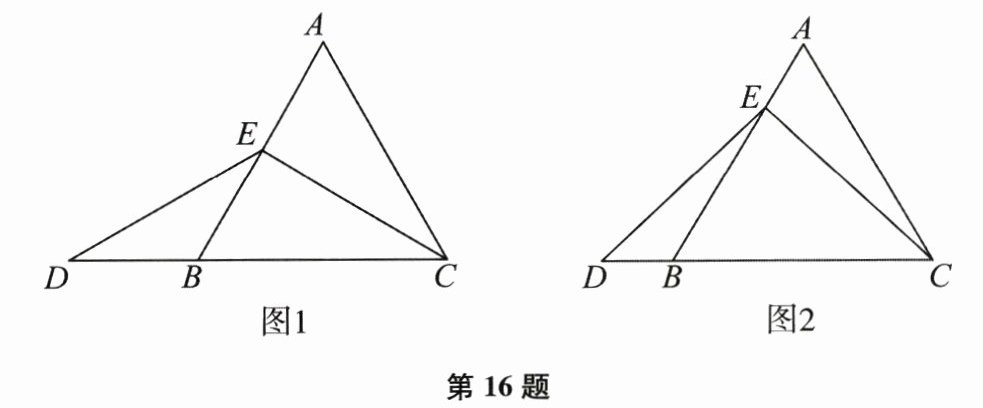
16. （本题12分）在等边三角形$ABC$中，点$E$在$AB$边上，点$D$在$CB$的延长线上，且$DE = EC$.
（1）如图1，当$E$为$AB$中点时，求证：$CB = 2BD$；
（2）如图2，若$AB = 12$，$AE = 2$，求$CD$的长.

答案：
16.解:
(1)
∵△ABC为等边三角形，
∴∠ABC=∠A=∠ACB=60°,
∵EB=AE,
∴CE⊥AB,CE是∠ACB的角平分线，
∴∠BEC=90°,∠BCE=30°,
∴2EB=BC,
∵ED=EC,
∴∠EDC=∠ECD=30°,
∴∠DEB=60°−30°=30°,
∴BD=BE,
∴2BD=BC.
(2)如图，过点E作EF//BC,交AC于点F,
∵△ABC为等边三角形，
∴∠AFE=∠ACB=∠ABC=60°，△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
　　
∴∠EDB=∠FEC,
　　在△BDE和△FEC中，
　　$\begin{cases} ∠EBD=∠EFC, \\ ∠EDB=∠FEC, \\ ED=EC, \end{cases}$
∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD,
∴CD=BC+BD=12+2=14.