《2025年伴你学单元达标测试卷八年级数学上册苏科版》

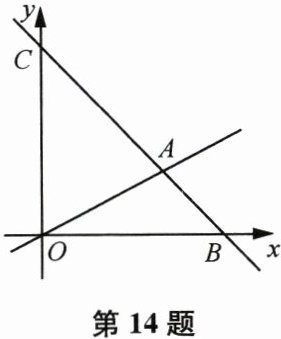
14. (本题12分)如图,在平面直角坐标系中,过点$B(6,0)$的直线$AB$与直线$OA$相交于点$A(4,2)$,直线$AB$交$y$轴于点$C$.
(1) 求直线$AB$的函数表达式;
(2) 求$\triangle OAC$的面积;
(3) 在线段$OA$或射线$AC$上找一点$M$,使$\triangle OMC$的面积是$\triangle OAC$的面积的$\frac{1}{4}$,求出此时点$M$的坐标.

答案： $14.(1)y=-x+6 (2)S_{\triangle OAC}=12 (3)M_1(1,\frac{1}{2}),M_2(1,5),M_3(-1,7)$

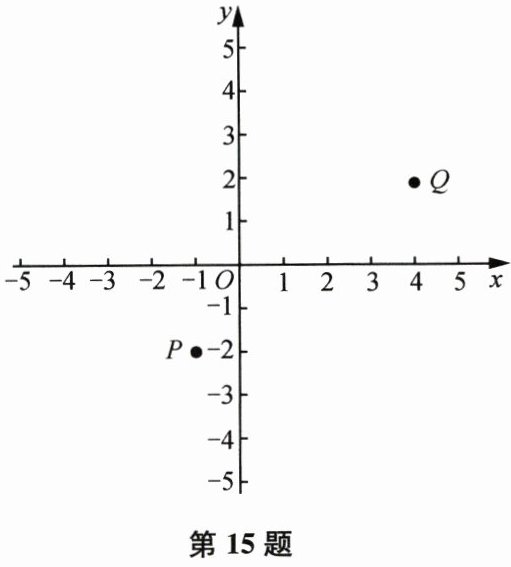
15. (本题12分)已知平面直角坐标平面内有点$P(-1,-2)$和点$Q(4,2)$.
(1) 取点$R(1,a)$,使$PR + RQ$为最小,求$a$的值;
(2) 取点$M(-2,m)$,使$PM + MQ$为最小,求$m$的值;
(3) 取点$N(-2,n)$,使$|NQ - NP|$为最大,求$n$的值.

答案： $15.(1)-\frac{2}{5} (2)-\frac{10}{7} (3)-\frac{14}{5}$