《2025年伴你学单元达标测试卷八年级数学上册苏科版》

25. (本题16分)(1) 如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=$\frac{1}{2}$∠BAD. 求证:EF=BE+FD.
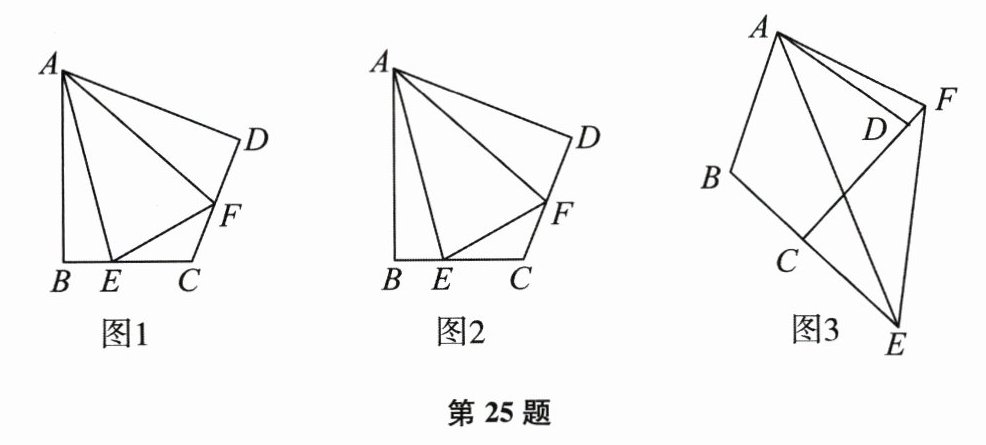
(2) 如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=$\frac{1}{2}$∠BAD,(1)中的结论是否仍然成立?
(3) 如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=$\frac{1}{2}$∠BAD,(1)中的结论是否仍然成立? 若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.

答案：
25. 证明：
(1) 延长$EB$到$G$，使$BG = DF$，连接$AG$.
$\because \angle ABG=\angle ABC=\angle D = 90^{\circ}$，$AB = AD$，
$\therefore \triangle ABG \cong \triangle ADF$.$\therefore AG = AF$，$\angle1=\angle2$.
$\therefore \angle1+\angle3=\angle2+\angle3=\angle EAF=\frac{1}{2}\angle BAD$.
$\therefore \angle GAE=\angle EAF$.
又$\because AE = AE$，$\therefore \triangle AEG \cong \triangle AEF$.$\therefore EG = EF$.
$\because EG = BE + BG$.$\therefore EF = BE + FD$
(2)
(1)中的结论$EF = BE + FD$仍然成立.
(3) 结论$EF = BE + FD$不成立，应当是$EF = BE - FD$.
证明：在$BE$上截取$BG$，使$BG = DF$，连接$AG$.
$\because \angle B+\angle ADC = 180^{\circ}$，$\angle ADF+\angle ADC = 180^{\circ}$，
$\therefore \angle B=\angle ADF$.
$\because AB = AD$，
$\therefore \triangle ABG \cong \triangle ADF$.
$\therefore \angle BAG=\angle DAF$，$AG = AF$.
$\therefore \angle BAG+\angle EAD=\angle DAF+\angle EAD$
$=\angle EAF=\frac{1}{2}\angle BAD$.
$\therefore \angle GAE=\angle EAF$.
$\because AE = AE$，
$\therefore \triangle AEG \cong \triangle AEF$.
$\therefore EG = EF$
$\because EG = BE - BG$
$\therefore EF = BE - FD$.