《2025年伴你学单元达标测试卷八年级数学上册苏科版》

7. 下列结论:①若三角形一边上的中线和这边上的高重合,则这个三角形是等腰三角形;②近似数3.1416的精确度是千分位;③三边分别为$\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$的三角形是直角三角形;④大于-$\sqrt{17}$而小于$\sqrt{11}$的所有整数的和为-4;⑤若一个直角三角形的两边长分别为3和4,则第三边长是5;其中正确的结论是①④(填序号).

答案： 7.①④

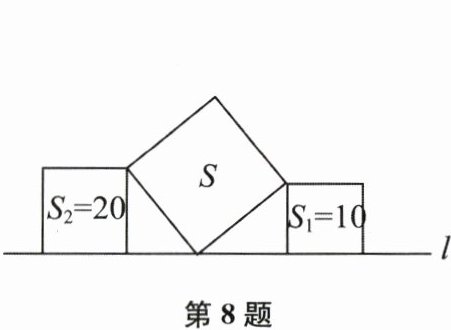
8. 三个正方形按图示位置摆放,S表示面积,则S的大小为30.

答案： 8.30

9. 所谓的勾股数就是指使等式a²+b²=c²成立的任何三个正整数.我国清代数学家罗士琳钻研出一种求勾股数的方法,对于任意正整数m、n(m ＞ n),取a=m²-n²,b=2mn,c=m²+n²,则a、b、c就是一组勾股数.请你结合这种方法,写出85(三个数中最大)、84和13组成一组勾股数.

答案： 9.13

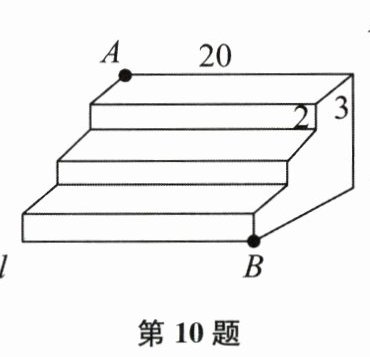
10. 如图,这是一个三级台阶,它的每一级的长、宽、高分别为20dm,3dm,2dm,A和B是这个台阶两个相对的端点,点A处有一只蚂蚁,想爬到点B处去吃可口的食物,则蚂蚁沿着台阶面爬到点B处的最短路径是25dm,确定最短路径的依据是两点之间，线段最短.

答案： 10.25 两点之间，线段最短

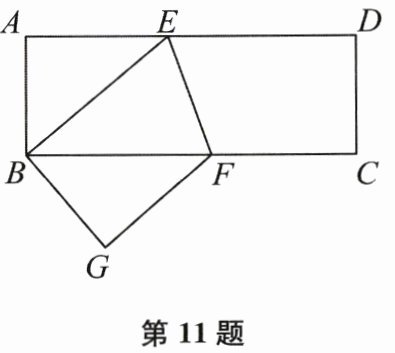
11. 已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为6.

答案： 11.6

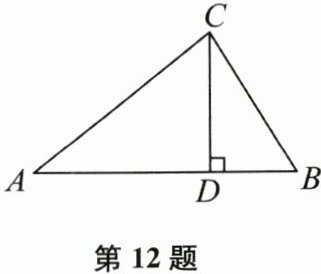
12. (本题8分)已知:如图,在△ABC中,CD⊥AB,垂足为点D,AC=20,BC=15,DB=9.
(1)求CD的长;
(2)求AB的长.

答案： 12.
(1)12
(2)25