《2025年伴你学单元达标测试卷八年级数学上册苏科版》

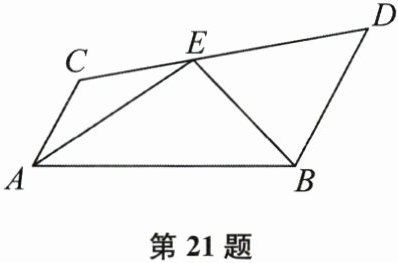
21. (本题12分)如图,已知AC//BD,EA、EB分别平分∠CAB和∠DBA,CD过点E,求证:AB=AC+BD.

答案：
21. 证明：在AB上取一点F，使$AF = AC$，连接EF.
$\because EA$、$EB$分别平分$\angle CAB$和$\angle DBA$，
$\therefore \angle CAE=\angle FAE$，$\angle EBF=\angle EBD$.
$\because AC// BD$，
$\therefore \angle C+\angle D = 180^{\circ}$.
在$\triangle ACE$和$\triangle AFE$中，
$\begin{cases} AC = AF, \\ \angle CAE = \angle FAE, \\ AE = AE, \end{cases}$
$\therefore \triangle ACE \cong \triangle AFE(SAS)$，
$\therefore \angle C=\angle AFE$.
$\because \angle AFE+\angle EFB = 180^{\circ}$，
$\therefore \angle EFB=\angle D$.
在$\triangle BEF$和$\triangle BED$中，
$\begin{cases} \angle EFB = \angle D, \\ \angle EBF = \angle EBD, \\ BE = BE, \end{cases}$
$\therefore \triangle BEF \cong \triangle BED(AAS)$，
$\therefore BF = BD$.
$\because AB = AF + BF$，
$\therefore AB = AC + BD$.

22. (本题14分)阅读材料:如果一个数的平方等于-1,记为$i^{2}=-1$,这个数i叫做虚数单位,那么形如a+bi(a,b为实数)的数就叫做复数,a叫这个复数的实部,b叫做这个复数的虚部.它有如下特点:
①它的加,减,乘法运算与整式的加,减,乘法运算类似,例如计算:
(2+i)+(3-4i)=(2+3)+(1-4)i=5-3i；(3+i)i=3i+i²=3i-1.
②若两个复数,它们的实部和虚部分别相等,则称这两个复数相等;若它们的实部相等,虚部互为相反数,则称这两个复数共轭:如1+2i的共轭复数为1-2i.
(1)填空:①(2+i)(2-i)=5；②(2+i)²=3 + 4i.
(2)若a+bi是(1+2i)²的共轭复数,求(b-a)²的值.

答案： 22. 解：
(1)①原式$=2^{2}-i^{2}=4-(-1)=4 + 1 = 5$；
②原式$=4 + 4i+i^{2}=4 + 4i-1=3 + 4i$；
故答案为：①$5$；②$3 + 4i$；
(2)$\because (1 + 2i)^{2}=1 + 4i-4=-3 + 4i$，$a + bi$是它的共轭复数，
$\therefore a=-3$，$b=-4$，
则原式$=(-4 + 3)^{2}=1$.