《2025年伴你学单元达标测试卷八年级数学上册苏科版》

9. 已知 $M$ 是满足不等式 $-\sqrt{2} ＜ a ＜ \pi$ 的所有整数的和,$N$ 是 $\sqrt{20}$ 的整数部分,则 $M + N$ 的平方根为 ±3.

答案： 9.±3

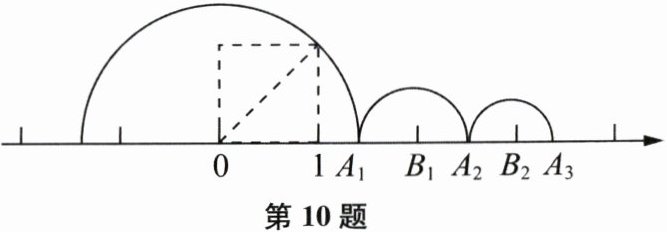
10. 如图,通过画边长为 $1$ 的正方形,就能准确的把 $\sqrt{2}$ 表示在数轴上点 $A_1$ 处,记 $A_1$ 右侧最近的整数点为 $B_1$,以点 $B_1$ 为圆心,$A_1B_1$ 为半径画半圆,交数轴于点 $A_2$,记 $A_2$ 右侧最近的整数点为 $B_2$,以点 $B_2$ 为圆心,$A_2B_2$ 为半径画半圆,交数轴于点 $A_3$,如此继续,则 $A_8B_8$ 的长为 $\sqrt{2}$ - 1.

答案： 10.$\sqrt{2}$ - 1

11. 计算:(1) $(\sqrt{3})^2 - 2^{-1} × (-4)$; (2) $\sqrt[3]{(-1)^2} + \sqrt[3]{-8} + \sqrt{3} - |1 - \sqrt{3}| + \sqrt{2}$.

答案： 11.
(1)5
(2)$\sqrt{2}$

12. 已知 $x - 2$ 的平方根是 $\pm 2$,$2x + y + 7$ 的立方根是 $3$,求 $x^2 + y^2$ 的算术平方根.

答案： 12.
∵x - 2的平方根是±2，
∴x - 2 = 4，解得x = 6。又
∵2x + y + 7的立方根是3，
∴2x + y + 7 = 27，解得y = 8，
∴x² + y² = 100，
∴x² + y²的算术平方根是10。

13. 若有一块长方形纸板和一块正方形纸板,其中长方形纸板的长为 $3\mathrm{dm}$,宽为 $2\mathrm{dm}$,且两块纸板的面积相等.
(1) 求正方形纸板的边长(结果保留根号);
(2) 能否在长方形纸板上截出两个完整的,且面积分别为 $2\mathrm{dm}^2$ 和 $3\mathrm{dm}^2$ 的正方形纸板? 判断并说明理由.(提示:$\sqrt{2} \approx 1.414$,$\sqrt{3} \approx 1.732$)

答案： 13.
(1)$\sqrt{6}$dm;
(2)不能，理由如下：
∵两个小正方形纸板的边长分别为$\sqrt{2}$dm，$\sqrt{3}$dm，边长和为$\sqrt{3}$ + $\sqrt{2}$≈1.732 + 1.414≈3.1(dm)，3.1dm＞3dm，
∴不能在长方形纸板上截出两个完整的，且面积分别为2dm²和3dm²的正方形纸板。