第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
14. 在学习《实数》时,我们思考了在方格网中画格点正方形的问题,如图是边长为 1 的方格网.
(1) 方格网中格点正方形的面积是
(2) 按照(1)中的思路,在方格网中设计图形,并求出线段$CD$的长.
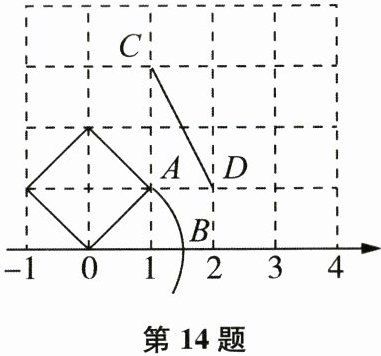
(1) 方格网中格点正方形的面积是
2
,由此可知,以原点为圆心,$OA$长为半径画弧,与数轴正半轴的交点$B$表示的数为$\sqrt{2}$
;说明无理数
可以在数轴上表示.(2) 按照(1)中的思路,在方格网中设计图形,并求出线段$CD$的长.

答案:
14.
(1)$2,\sqrt{2}$,无理数.
(2)构造为$CD$边的格点正方形$CDMN$,$\because S_{正方形CDMN}=4×\frac{1}{2}×1×2+1×1=5$,$\therefore CD^{2}=5$,$\therefore CD=\sqrt{5}$.
(1)$2,\sqrt{2}$,无理数.
(2)构造为$CD$边的格点正方形$CDMN$,$\because S_{正方形CDMN}=4×\frac{1}{2}×1×2+1×1=5$,$\therefore CD^{2}=5$,$\therefore CD=\sqrt{5}$.
15. 阅读材料:
材料一:大家知道$\sqrt{5}$是无理数,而无理数是无限不循环小数,因此$\sqrt{5}$的小数部分我们不可能全部地写出来,于是明明用$\sqrt{5}-2$来表示$\sqrt{5}$的小数部分,你同意明明的表示方法吗? 事实上,明明的表示方法是有道理的,因为$\sqrt{5}$的整数部分是 2,用$\sqrt{5}$减去其整数部分,差就是小数部分.
由此可得:如果$\sqrt{5}=x+y$,其中$x$是整数,且$0<y<1$,那么$x=2,y=\sqrt{5}-2$.
其中$x$就是$\sqrt{5}$的整数部分,$y$就是$\sqrt{5}$的小数部分.
材料二:已知$m,n$是有理数,且满足等式$2-\sqrt{7}m=\frac{2}{5}\sqrt{7}+3n-m$,则可求出$m,n$的值.
求解过程如下:
$\because2-\sqrt{7}m=\frac{2}{5}\sqrt{7}+3n-m$,
$\therefore2-\sqrt{7}\cdot m=(3n-m)+\sqrt{7}×\frac{2}{5}$.
$\because m,n$是有理数,
$\therefore2=3n-m,-m=\frac{2}{5}$,
解得:$m=-\frac{2}{5},n=\frac{8}{15}$.
根据以上材料,解答下列问题:
(1) 如果$\sqrt{13}=a+b$,其中$a$是整数,且$0<b<1$,那么$a=$
(2) 如果$8+\sqrt{19}$的小数部分为$m,8-\sqrt{19}$的整数部分为$n$,求$m-n-\sqrt{19}$的值;
(3) 已知$x,y$是有理数,且满足等式$4(x-2)^2-3y-\sqrt{3}y=34+3\sqrt{3}$,求$x+y$的值.
材料一:大家知道$\sqrt{5}$是无理数,而无理数是无限不循环小数,因此$\sqrt{5}$的小数部分我们不可能全部地写出来,于是明明用$\sqrt{5}-2$来表示$\sqrt{5}$的小数部分,你同意明明的表示方法吗? 事实上,明明的表示方法是有道理的,因为$\sqrt{5}$的整数部分是 2,用$\sqrt{5}$减去其整数部分,差就是小数部分.
由此可得:如果$\sqrt{5}=x+y$,其中$x$是整数,且$0<y<1$,那么$x=2,y=\sqrt{5}-2$.
其中$x$就是$\sqrt{5}$的整数部分,$y$就是$\sqrt{5}$的小数部分.
材料二:已知$m,n$是有理数,且满足等式$2-\sqrt{7}m=\frac{2}{5}\sqrt{7}+3n-m$,则可求出$m,n$的值.
求解过程如下:
$\because2-\sqrt{7}m=\frac{2}{5}\sqrt{7}+3n-m$,
$\therefore2-\sqrt{7}\cdot m=(3n-m)+\sqrt{7}×\frac{2}{5}$.
$\because m,n$是有理数,
$\therefore2=3n-m,-m=\frac{2}{5}$,
解得:$m=-\frac{2}{5},n=\frac{8}{15}$.
根据以上材料,解答下列问题:
(1) 如果$\sqrt{13}=a+b$,其中$a$是整数,且$0<b<1$,那么$a=$
3
,$b=$$\sqrt{13}-3$
;(2) 如果$8+\sqrt{19}$的小数部分为$m,8-\sqrt{19}$的整数部分为$n$,求$m-n-\sqrt{19}$的值;
(3) 已知$x,y$是有理数,且满足等式$4(x-2)^2-3y-\sqrt{3}y=34+3\sqrt{3}$,求$x+y$的值.
答案:
15.
(1)$3,\sqrt{13}-3$.
(2)$\because8+\sqrt{19}$的小数部分为$m$,$8-\sqrt{19}$的整数部分为$n$,$4<\sqrt{19}<5$,$\therefore m=\sqrt{19}-4$,$n=3$,$\therefore m-n-\sqrt{19}=\sqrt{19}-4-3-\sqrt{19}=-7$.
(3)$x,y$满足等式$4(x-2)^{2}-3y-\sqrt{3}y=34+3\sqrt{3}$,$\therefore4(x-2)^{2}-3y=34$,$-y=3$,$\therefore y=-3$,$\therefore4(x-2)^{2}+9=34$,$\therefore x=-\frac{1}{2}$或$x=\frac{9}{2}$,当$x=-\frac{1}{2},y=-3$时,$x+y=-\frac{1}{2}-3=-\frac{7}{2}$;当$x=\frac{9}{2},y=-3$时,$x+y=\frac{9}{2}-3=\frac{3}{2}$,综上所述,$x+y$的值为$-\frac{7}{2}$或$\frac{3}{2}$.
(1)$3,\sqrt{13}-3$.
(2)$\because8+\sqrt{19}$的小数部分为$m$,$8-\sqrt{19}$的整数部分为$n$,$4<\sqrt{19}<5$,$\therefore m=\sqrt{19}-4$,$n=3$,$\therefore m-n-\sqrt{19}=\sqrt{19}-4-3-\sqrt{19}=-7$.
(3)$x,y$满足等式$4(x-2)^{2}-3y-\sqrt{3}y=34+3\sqrt{3}$,$\therefore4(x-2)^{2}-3y=34$,$-y=3$,$\therefore y=-3$,$\therefore4(x-2)^{2}+9=34$,$\therefore x=-\frac{1}{2}$或$x=\frac{9}{2}$,当$x=-\frac{1}{2},y=-3$时,$x+y=-\frac{1}{2}-3=-\frac{7}{2}$;当$x=\frac{9}{2},y=-3$时,$x+y=\frac{9}{2}-3=\frac{3}{2}$,综上所述,$x+y$的值为$-\frac{7}{2}$或$\frac{3}{2}$.
查看更多完整答案,请扫码查看


