《2025年全效学习阶段发展评价九年级数学全一册浙教版》

1. [原创]二次函数 $ y = (x + 2)^2 $ 的图象大致是(D)

答案： D

2. [教材 P12 例 2 改编]下列关于函数 $ y = -\frac{1}{2}(x + 3)^2 + 2 $ 图象的说法,正确的是(D)
A.开口向上
B.对称轴是直线 $ x = 3 $
C.有最低点
D.顶点坐标为 $ (-3, 2) $

答案： D

3. [教材 P14 课内练习 T2 改编]把下表补充完整：

答案： 填表如下：
抛物线 开口方向 对称轴 顶点坐标
$y=2(x-1)^{2}$ 向上 直线$x=1$ $(1,0)$
$y=\frac {2}{3}x^{2}-7$ 向上 y轴 $(0,-7)$
$y=-2(x+2)^{2}-5$ 向下 直线$x=-2$ $(-2,-5)$

4. (1)把抛物线 $ y = 2x^2 $ 向下平移 1 个单位,得到的抛物线的函数表达式为$y=2x^{2}-1$.
(2)把抛物线 $ y = 2x^2 + 1 $ 向左平移 1 个单位,再向下平移 3 个单位,得到的抛物线的函数表达式为$y=2x^{2}+4x$.
(3)把抛物线 $ y = (x - 1)^2 + 3 $ 向左平移 1 个单位,再向下平移 3 个单位,得到的抛物线的函数表达式为$y=x^{2}$.

答案：
(1)$y=2x^{2}-1$
(2)$y=2x^{2}+4x$
(3)$y=x^{2}$

5. 在同一平面直角坐标系中,画出函数 $ y = x^2 $,$ y = (x + 2)^2 $,$ y = (x - 2)^2 $ 的图象,并写出它们的对称轴及顶点坐标.

答案：
解:画出函数图象如答图所示.

抛物线$y=x^{2}$的对称轴是y轴,顶点坐标为$(0,0)$；抛物线$y=(x+2)^{2}$的对称轴是直线$x=-2$,顶点坐标为$(-2,0)$；抛物线$y=(x-2)^{2}$的对称轴是直线$x=2$,顶点坐标为$(2,0)$.

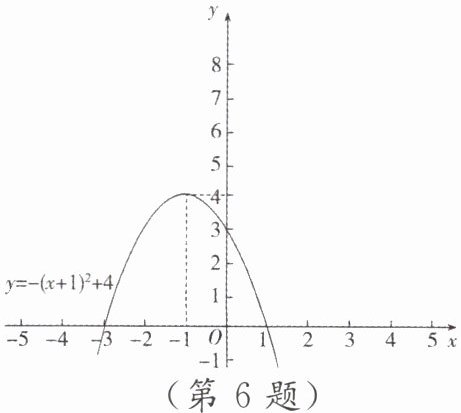
6. [教材 P12 例 2 改编]已知二次函数 $ y = -(x + 1)^2 + 4 $ 的图象如图所示,把此函数图象向右平移 3 个单位,向上平移 3 个单位,请求出平移后的函数表达式,并在同一平面直角坐标系中画出平移后的函数图象.

答案：
解:平移后的函数表达式为$y=-(x-2)^{2}+7$,画出函数图象如答图所示.