1. 某商场举办有奖销售活动,每张奖券被抽中的可能性相同,若以每 1 000 张奖券为一个开奖单位,设 5 个一等奖,15 个二等奖,不设其他奖项,则只抽 1 张奖券恰好中奖的概率是
$\frac{1}{50}$
.
答案:
$\frac{1}{50}$
2. [教材 P63 目标与评定 T15 改编]有 A,B,C 三种款式的衣服,E,F,G 三种款式的裤子,小江任意选一件衣服和一条裤子.
(1)请用列表或画树状图的方法表示出所有可能的搭配方式.
(2)求恰好选中 A 款衣服和 E 款裤子的概率.
(1)请用列表或画树状图的方法表示出所有可能的搭配方式.
(2)求恰好选中 A 款衣服和 E 款裤子的概率.
答案:
解:
(1)画树状图如答图所示.

(2)由答图可知,共有9种等可能的结果,其中恰好选中A款衣服和E款裤子的有1种,
$\therefore$恰好选中A款衣服和E款裤子的概率是$\frac{1}{9}$.
解:
(1)画树状图如答图所示.

(2)由答图可知,共有9种等可能的结果,其中恰好选中A款衣服和E款裤子的有1种,
$\therefore$恰好选中A款衣服和E款裤子的概率是$\frac{1}{9}$.
3. [教材 P57 例 1 改编]某公司年会举行抽奖活动,共准备了 100 张奖券,设一等奖 5 张,二等奖 20 张,三等奖 50 张,每人限抽 1 张,每张奖券大小、形状都相同.
(1)求第一个抽奖者抽到一等奖的概率.
(2)若第一个抽奖者抽走了 1 张三等奖,求第二个抽奖者抽到三等奖的概率.
(1)求第一个抽奖者抽到一等奖的概率.
(2)若第一个抽奖者抽走了 1 张三等奖,求第二个抽奖者抽到三等奖的概率.
答案:
解:
(1)$\because$共准备了100张奖券,设一等奖5张,二等奖20张,三等奖50张,
$\therefore$第一个抽奖者抽到一等奖的概率是$\frac{5}{100}=\frac{1}{20}$.
(2)$\because$第一个抽奖者抽走了1张三等奖,则剩下99张奖券中,三等奖还有49张,
$\therefore$第二个抽奖者抽到三等奖的概率是$\frac{49}{99}$.
(1)$\because$共准备了100张奖券,设一等奖5张,二等奖20张,三等奖50张,
$\therefore$第一个抽奖者抽到一等奖的概率是$\frac{5}{100}=\frac{1}{20}$.
(2)$\because$第一个抽奖者抽走了1张三等奖,则剩下99张奖券中,三等奖还有49张,
$\therefore$第二个抽奖者抽到三等奖的概率是$\frac{49}{99}$.
4. [教材 P58 课内练习 T1 改编]某保险公司的一张关于某地区人口寿命的表格,现摘录部分内容如下表所示:
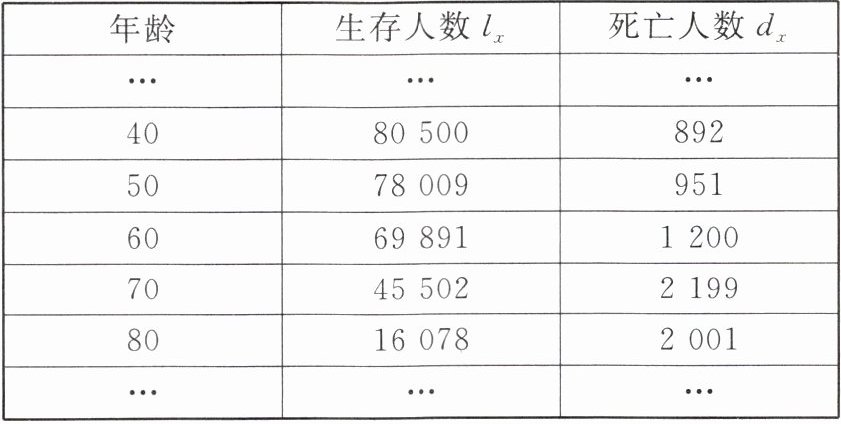
根据上述信息,请回答下列问题:
(1)某人今年 50 岁,他当年死亡的概率是多少?他活到 80 岁的概率是多少(结果精确到 0.000 1)?
(2)若有 20 000 名 50 岁的人参加寿险投保,当年死亡的人均赔偿金为 20 万元,则估计保险公司需支付当年死亡的人的赔偿金为多少万元(结果精确到百位)?

根据上述信息,请回答下列问题:
(1)某人今年 50 岁,他当年死亡的概率是多少?他活到 80 岁的概率是多少(结果精确到 0.000 1)?
(2)若有 20 000 名 50 岁的人参加寿险投保,当年死亡的人均赔偿金为 20 万元,则估计保险公司需支付当年死亡的人的赔偿金为多少万元(结果精确到百位)?
答案:
解:
(1)$P$(50岁死亡)$=\frac{951}{78009}\approx0.0122$,
$P$(活到80岁)$=\frac{16078}{78009}\approx0.2061$.
答:他当年死亡的概率约是0.0122,他活到80岁的概率约是0.2061.
(2)$0.0122×20000×20\approx4900$(万元).
答:估计保险公司需支付当年死亡的人的赔偿金为4900万元.
(1)$P$(50岁死亡)$=\frac{951}{78009}\approx0.0122$,
$P$(活到80岁)$=\frac{16078}{78009}\approx0.2061$.
答:他当年死亡的概率约是0.0122,他活到80岁的概率约是0.2061.
(2)$0.0122×20000×20\approx4900$(万元).
答:估计保险公司需支付当年死亡的人的赔偿金为4900万元.
查看更多完整答案,请扫码查看


