《2025年全效学习阶段发展评价九年级数学全一册浙教版》

7. 如图,在$□ ABCD$中,对角线$AC$,$BD相交于点O$. 若$AB = 4$,$BD = 10$,$\sin \angle BDC= \frac{3}{5}$,则$□ ABCD$的面积为______.
]

答案：
24　[解析]如答图,过点C作CE ⊥BD于点E.　　　 　易知$CD=AB=4$,
∴在$Rt\triangle CDE$中,　$CE=CD\cdot\sin \angle BDC=\frac{12}{5}$.　又
∵$BD=10$,$\therefore S_{□ ABCD}=2× \frac{1}{2}BD\cdot CE=24$.

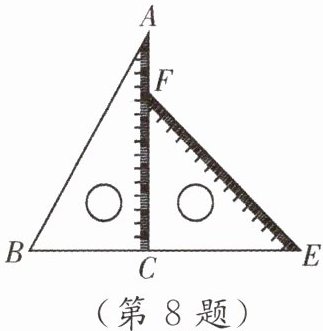
8. 数学拓展课程《玩转学具》课堂中,小陆同学发现：一副三角尺中,含$45^{\circ}角的三角尺的斜边与含30^{\circ}$角的三角尺的长直角边相等,于是,小陆同学提出了一个问题：将一副三角尺的直角顶点重合,按如图所示的方式摆放在一起,点$B$,$C$,$E$在同一条直线上. 若$BC = 6$,求$AF$的长. 请你运用所学的数学知识解决这个问题.
]

答案： 解:在$Rt\triangle ABC$中,$BC=6$,$\angle A =30^{\circ}$,
∴$AC=\frac{BC}{\tan A}=6\sqrt{3}$,
∴$EF=AC=6\sqrt{3}$.
∵$\angle E=45^{\circ}$,
∴$FC=EF\cdot\sin E=3\sqrt{6}$,
∴$AF=AC - FC=6\sqrt{3}-3\sqrt{6}$.

9. 如图,在$\triangle ABC$中,$BC = 12$,$\tan A= \frac{3}{4}$,$\angle B = 30^{\circ}$. 求$AC和AB$的长.
]

答案：
解:如答图,过点C作CD⊥AB于点D.　　　 　在$Rt\triangle BCD$中,$\angle B=30^{\circ}$,$BC=12$,
∴$CD=BC\cdot\sin B=6$,　$BD=BC\cdot\cos B=6\sqrt{3}$.　在$Rt\triangle ACD$中,$\tan A=\frac{3}{4}$,
∴$AD=\frac{CD}{\tan A}=8$,
∴$AC=\sqrt{AD^{2}+CD^{2}}=10$,　$AB=AD + BD=8+6\sqrt{3}$.

10. [教材P19作业题T6改编]在一张矩形纸片$ABCD$中,$AD = 5\mathrm{cm}$,$AB = 4\mathrm{cm}$,现将这张纸片按如图所示的方式折叠,请分别求出折痕的长.
(1)如图①,点$B落在AD上的点F$处,折痕为$AE$.
(2)如图②,$P$,$Q分别是AB$,$CD$的中点,点$B落在PQ上的点F$处,折痕为$AE$.
]

答案： 解:
(1)由折叠,得$\angle FAE = \angle BAE$.
∵四边形ABCD是矩形，
∴$\angle FAB=\angle B=90^{\circ}$,
∴$\angle EAB=45^{\circ}$.　　在$Rt\triangle ABE$中,$AB=4cm$,
∴$AE=\frac{AB}{\cos \angle EAB}=4\sqrt{2}cm$.　　
(2)
∵四边形ABCD是矩形,且P,Q分别是AB,CD的中点，
∴$AD// PQ// BC$,$DQ=CQ$,
∴$AG=GE$,$\angle DAF=\angle AFG$,由折叠,得$\angle AFE=\angle B=90^{\circ}$,$\angle FAG=\angle BAE$.
∵FG是直角$\triangle AFE$斜边上的中线,
∴$FG = AG$,$\therefore \angle AFG = \angle FAG$,
∴$\angle DAF=\angle FAG=\angle BAE =30^{\circ}$.　　在$Rt\triangle ABE$中,$AB=4cm$,
∴$AE=\frac{AB}{\cos \angle BAE}=\frac{8\sqrt{3}}{3}cm$.