《2025年全效学习阶段发展评价九年级数学全一册浙教版》

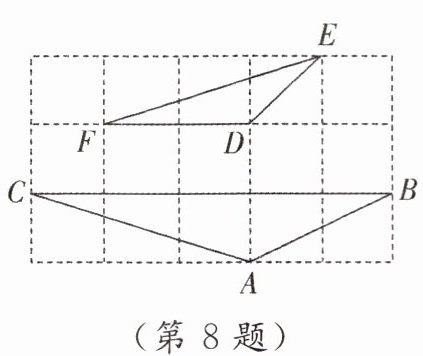
8. 如图,在正方形网格中,△ABC∽△DEF,则∠BAC 的度数为135°.

答案： $135^{\circ }$【解析】易知$∠EDH=45^{\circ },$$\therefore ∠EDF=135^{\circ }.$$\because △ABC\backsim △DEF,$$\therefore ∠BAC=∠EDF=135^{\circ }.$

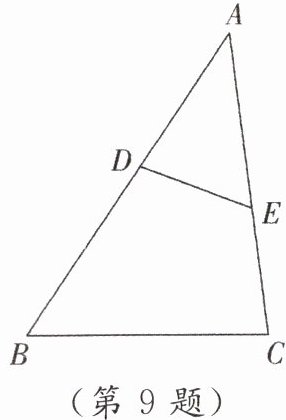
9. 如图,△ABC∽△AED,AD = 5 cm,BD = 6 cm,AC = 9 cm,则 AE = $\frac {55}{9}$cm,△ABC 与△AED 的相似比是$\frac {9}{5}$.

答案： $\frac {55}{9}$$\frac {9}{5}$【解析】$\because AD=5cm,$$BD=6cm,$$\therefore AB=AD+BD=11cm.$$\because △ABC\backsim △AED,$$\therefore \frac {AD}{AC}=\frac {AE}{AB}$,即$\frac {5}{9}=\frac {AE}{11},$$\therefore AE=\frac {55}{9}cm.$$\because △ABC\backsim △AED,$$\therefore △ABC$与$△AED$的相似比是$\frac {AC}{AD}=\frac {9}{5}.$

10. 如图,D 是 AB 的中点,△ABC∽△ACD,且 AD = 2,∠ADC = 65°.
(1) 写出△ABC 与△ACD 的对应边成比例的比例式.
(2) 求 AC 的长及∠ACB 的度数.

答案： 解:
(1)$\because △ABC\backsim △ACD,$$\therefore \frac {AD}{AC}=\frac {AC}{AB}=\frac {CD}{BC}.$
(2)$\because AD=2$,D 是 AB 的中点,$\therefore AB=4.$由
(1),得$\frac {AD}{AC}=\frac {AC}{AB},\therefore \frac {2}{AC}=\frac {AC}{4},$$\therefore AC=2\sqrt {2}$(负值舍去).$\because △ABC\backsim △ACD,$$\therefore ∠ACB=∠ADC=65^{\circ }.$

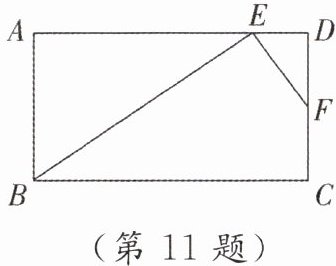
11. 如图,在矩形 ABCD 中,点 E,F 分别在 AD,DC 上,△ABE∽△DEF,AB = 6,AE = 9,DE = 2. 求 EF 的长.

答案： 解:在$Rt△ABE$中,$\because AB=6,$$AE=9,∠A=90^{\circ },\therefore BE=$$\sqrt {AB^{2}+AE^{2}}=3\sqrt {13}.$$\because △ABE\backsim △DEF,$$\therefore \frac {EF}{BE}=\frac {DE}{AB}$,即$\frac {EF}{3\sqrt {13}}=\frac {2}{6},$$\therefore EF=\sqrt {13}.$

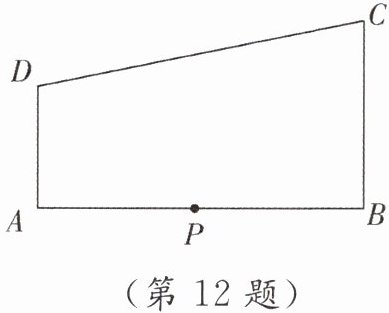
12. 如图,AD//BC,∠B = 90°,AB = 8,AD = 3,BC = 4,P 为 AB 上一动点. 若△PAD 与△PBC 是相似三角形,求 AP 的长.

答案： 解:$\because AD// BC,$$\therefore ∠A=180^{\circ }-∠B=90^{\circ },$$\therefore ∠A=∠B=90^{\circ }.$设$AP=x$,则$BP=8-x.$分两种情况讨论：①若$△APD\backsim △BPC$,则 AP :$BP=AD:BC,$即$x:(8-x)=3:4$,解得x$=\frac {24}{7}.$②若$△APD\backsim △BCP$,则 AP :$BC=AD:BP,$即$x:4=3:(8-x)$,解得$x=2$或$x=6.$综上所述,$AP=\frac {24}{7}$或2或6.