《2025年全效学习阶段发展评价九年级数学全一册浙教版》

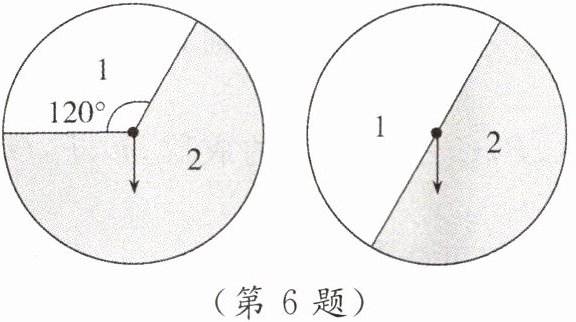
6. [教材P49例5改编]如图是两个可以自由转动的转盘,每个转盘被分成两个扇形,同时转动两个转盘,转盘停止后,指针所指区域内的数字之和为4的概率是( )

A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{5}$

答案：
B【解析】在第一个转盘中,"2"对应的圆心角为$240^{\circ }$,是"1"对应的圆心角的2倍,把转盘划分成等大的3份,相当于"2"占两份,"1"占一份,画树状图如答图所示. 由答图可知,共有6种等可能的结果,其中数字之和为4的有2种,
∴数字之和为4的概率是$\frac{2}{6}=\frac{1}{3}.$

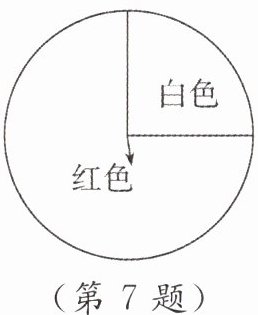
7. [教材P51作业题T2改编]如图,转盘的白色扇形和红色扇形的圆心角分别为90°和270°,让转盘自由转动2次,指针第一次落在红色区域,第二次落在白色区域的概率是______.

答案：
$\frac{3}{16}$【解析】
∵白色扇形的圆心角为$90^{\circ }$,红色扇形的圆心角为$270^{\circ },$
∴白色扇形的面积：红色扇形的面积$=\frac{1}{3}.$画树状图如答图所示. 由答图可知,共有16种等可能的结果,其中指针第一次落在红色区域,第二次落在白色区域的有3种,
∴让转盘自由转动两次,指针第一次落在红色区域,第二次落在白色区域的概率是$\frac{3}{16}.$

8. 一天晚上,小伟帮妈妈清洗茶杯,三个茶杯只有颜色不同,其中一个无盖,突然停电了,小伟只好把杯盖与茶杯随机地搭配在一起,则搭配完全正确的概率是______.

答案：
$\frac{1}{6}$【解析】设3个茶杯分别为A,B,C,A的杯盖是a,B的杯盖是b,C无盖,画树状图如答图所示. 共有6种等可能的结果,其中搭配完全正确的有1种,
∴搭配完全正确的概率是$\frac{1}{6}.$

9. [教材P51作业题T5改编]华东地区N市和S市之间每天有往返飞机航班各2趟. 甲、乙两人同一天从N市飞往S市,第二天又从S市飞回N市. 若他们可选择任一航班往返,则选择同一航班从N市飞往S市,再选择不同航班从S市飞回N市的概率是多少？

答案： 解:设从N市飞往S市的航班为A,B,从S市飞往N市的航班为a,b.列表如下:乙选的甲选的航班　A,a A,b B,a B,b A,a　AAaa, AAab, ABaa, ABab,A,b B,a B,b　BAba, BAbb, BBba, BBbb,由表可知,共有16种等可能的结果,其中甲、乙两人选择同一航班从N市飞往S市,再选择不同航班从S市飞回N市的有4种,
∴概率是$\frac{4}{16}=\frac{1}{4}.$

10. 在3张相同的小纸条上,分别写上条件：①四边形ABCD是菱形；②四边形ABCD有一个内角是直角；③四边形ABCD的对角线相等. 将这3张小纸条做成3支签,放在一个不透明的盒子中.
(1)搅匀后从中任意抽出1支签,抽到条件①的概率是______.
(2)搅匀后先从中任意抽出1支签(不放回),再从余下的2支签中任意抽出1支签,四边形ABCD同时满足抽到的2张小纸条上的条件,求四边形ABCD一定是正方形的概率.

答案：

(1)$\frac{1}{3}$
(2)解:画树状图如答图所示. 由答图可知,共有6种等可能的结果,其中恰好使四边形ABCD一定是正方形的有4种,
∴四边形ABCD一定是正方形的概率是$\frac{4}{6}=\frac{2}{3}.$