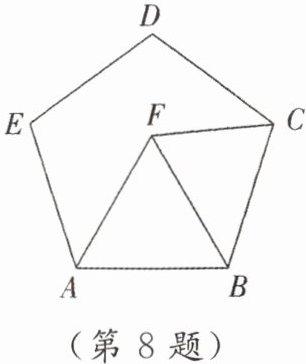
8. 如图,点 $F$ 在正五边形 $ABCDE$ 的内部,$\triangle ABF$ 为等边三角形,则 $\angle AFC$ 的度数为(
A.$108^{\circ}$
B.$120^{\circ}$
C.$126^{\circ}$
D.$132^{\circ}$
C
)
A.$108^{\circ}$
B.$120^{\circ}$
C.$126^{\circ}$
D.$132^{\circ}$
答案:
C [解析]
∵五边形$ABCDE$是正五边形,
∴$\angle ABC=108^{\circ}$,$AB =BC$.
∵$\triangle ABF$为等边三角形,
∴$\angle ABF=\angle AFB=60^{\circ}$,$AB =BF$,
∴$BF=BC$,$\angle CBF=\angle ABC−\angle ABF=48^{\circ}$,
∴$\angle BFC=\frac{1}{2}×(180^{\circ}-\angle CBF)=66^{\circ}$,
∴$\angle AFC=\angle BFC+\angle AFB =126^{\circ}$.
∵五边形$ABCDE$是正五边形,
∴$\angle ABC=108^{\circ}$,$AB =BC$.
∵$\triangle ABF$为等边三角形,
∴$\angle ABF=\angle AFB=60^{\circ}$,$AB =BF$,
∴$BF=BC$,$\angle CBF=\angle ABC−\angle ABF=48^{\circ}$,
∴$\angle BFC=\frac{1}{2}×(180^{\circ}-\angle CBF)=66^{\circ}$,
∴$\angle AFC=\angle BFC+\angle AFB =126^{\circ}$.
9. 半径为 2 的圆内接正三角形、正方形、正六边形的边心距(外接圆的圆心到正多边形的边的距离)之比为
$1:\sqrt{2}:\sqrt{3}$
.
答案:
$1:\sqrt{2}:\sqrt{3}$
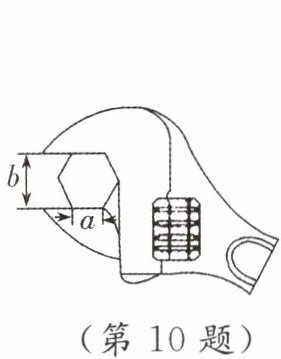
10. 如图,在拧开一个边长为 $a$ 的正六角形螺帽时,扳手张开的开口 $b = 20$ mm,则边长 $a= $______mm.

答案:
$\frac{20\sqrt{3}}{3}$ [解析]如答图,连结$OC$,$OD$,过点$O$作$OH\perp CD$于点$H$.

∵$\angle COD=60^{\circ}$,$OC=OD$,$OH \perp CD$,
∴$\angle COH=\frac{1}{2}\angle COD=30^{\circ}$,
$CH=DH=\frac{1}{2}CD$,
∴$OC=2CH$.
易知$OH=\frac{1}{2}b=10mm$,$OH^{2}+CH^{2}=OC^{2}$,
∴$10^{2}+CH^{2}=(2CH)^{2}$,
∴$CH=\frac{10\sqrt{3}}{3}mm$(负值舍去),
∴$a=2CH=\frac{20\sqrt{3}}{3}mm$.
$\frac{20\sqrt{3}}{3}$ [解析]如答图,连结$OC$,$OD$,过点$O$作$OH\perp CD$于点$H$.

∵$\angle COD=60^{\circ}$,$OC=OD$,$OH \perp CD$,
∴$\angle COH=\frac{1}{2}\angle COD=30^{\circ}$,
$CH=DH=\frac{1}{2}CD$,
∴$OC=2CH$.
易知$OH=\frac{1}{2}b=10mm$,$OH^{2}+CH^{2}=OC^{2}$,
∴$10^{2}+CH^{2}=(2CH)^{2}$,
∴$CH=\frac{10\sqrt{3}}{3}mm$(负值舍去),
∴$a=2CH=\frac{20\sqrt{3}}{3}mm$.
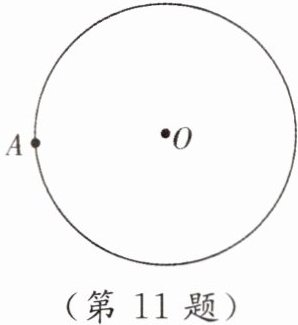
11. 如图,已知 $\odot O$ 和 $\odot O$ 上的一点 $A$,请回答下列问题:
(1) 作 $\odot O$ 的内接正六边形 $ABCDEF$(不写作法,保留作图痕迹).
(2) 连结 $BF$,$CE$,判断四边形 $BCEF$ 的形状,并加以证明.
(1) 作 $\odot O$ 的内接正六边形 $ABCDEF$(不写作法,保留作图痕迹).
(2) 连结 $BF$,$CE$,判断四边形 $BCEF$ 的形状,并加以证明.

答案:
解:
(1)作图如答图①所示.

(2)四边形$BCEF$是矩形.证明如下:
如答图②.
∵六边形$ABCDEF$是正六边形,
∴$\angle EDC=\angle FED=120^{\circ}$,$AB=AF=DE=DC$,$FE=BC$,
∴$\overset{\frown}{AB}=\overset{\frown}{AF}=\overset{\frown}{DE}=\overset{\frown}{DC}$,
∴$\overset{\frown}{BF}=\overset{\frown}{CE}$,$\therefore BF=CE$,
∴四边形$BCEF$是平行四边形.
∵$DE=DC$,$\angle EDC=120^{\circ}$,
∴$\angle DEC=\angle DCE=30^{\circ}$,
∴$\angle CEF=\angle FED−\angle DEC =90^{\circ}$,
∴四边形$BCEF$是矩形.
解:
(1)作图如答图①所示.

(2)四边形$BCEF$是矩形.证明如下:
如答图②.
∵六边形$ABCDEF$是正六边形,
∴$\angle EDC=\angle FED=120^{\circ}$,$AB=AF=DE=DC$,$FE=BC$,
∴$\overset{\frown}{AB}=\overset{\frown}{AF}=\overset{\frown}{DE}=\overset{\frown}{DC}$,
∴$\overset{\frown}{BF}=\overset{\frown}{CE}$,$\therefore BF=CE$,
∴四边形$BCEF$是平行四边形.
∵$DE=DC$,$\angle EDC=120^{\circ}$,
∴$\angle DEC=\angle DCE=30^{\circ}$,
∴$\angle CEF=\angle FED−\angle DEC =90^{\circ}$,
∴四边形$BCEF$是矩形.
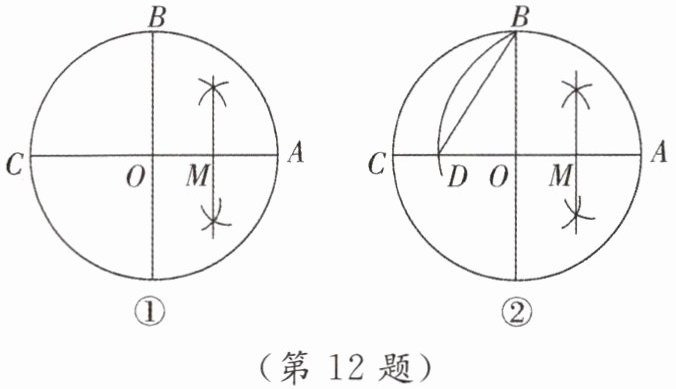
12. 小敏在作 $\odot O$ 的内接正五边形时,先做了如下几个步骤:(1) 作 $\odot O$ 的两条互相垂直的直径,再作 $OA$ 的垂直平分线交 $OA$ 于点 $M$,如图①;(2) 以点 $M$ 为圆心,$BM$ 长为半径作圆弧,交 $CA$ 于点 $D$,连结 $BD$,如图②. 若 $\odot O$ 的半径为 1,则由上述作图得到的关于正五边形的边长 $BD$ 的等式为( )
A.$BD^2= \frac{\sqrt{5}-1}{2}OD$
B.$BD^2= \frac{\sqrt{5}+1}{2}OD$
C.$BD^2= \sqrt{5}OD$
D.$BD^2= \frac{\sqrt{5}}{2}OD$

A.$BD^2= \frac{\sqrt{5}-1}{2}OD$
B.$BD^2= \frac{\sqrt{5}+1}{2}OD$
C.$BD^2= \sqrt{5}OD$
D.$BD^2= \frac{\sqrt{5}}{2}OD$
答案:
C [解析]如答图,连结$BM$.

由题意,得$OB=OA=1$,$AD\perp OB$,$BM=DM$.
∵$OA$的垂直平分线交$OA$于点$M$,
∴$OM=AM=\frac{1}{2}OA=\frac{1}{2}$,
∴$BM=\sqrt{OM^{2}+OB^{2}}=\frac{\sqrt{5}}{2}$,
∴$DM=\frac{\sqrt{5}}{2}$,
∴$OD=DM−OM=\frac{\sqrt{5}}{2}-\frac{1}{2}=\frac{\sqrt{5}-1}{2}$,
∴$BD^{2}=OD^{2}+OB^{2}=\frac{5-\sqrt{5}}{2}=\frac{\sqrt{5}(\sqrt{5}-1)}{2}=\sqrt{5}OD$.
C [解析]如答图,连结$BM$.

由题意,得$OB=OA=1$,$AD\perp OB$,$BM=DM$.
∵$OA$的垂直平分线交$OA$于点$M$,
∴$OM=AM=\frac{1}{2}OA=\frac{1}{2}$,
∴$BM=\sqrt{OM^{2}+OB^{2}}=\frac{\sqrt{5}}{2}$,
∴$DM=\frac{\sqrt{5}}{2}$,
∴$OD=DM−OM=\frac{\sqrt{5}}{2}-\frac{1}{2}=\frac{\sqrt{5}-1}{2}$,
∴$BD^{2}=OD^{2}+OB^{2}=\frac{5-\sqrt{5}}{2}=\frac{\sqrt{5}(\sqrt{5}-1)}{2}=\sqrt{5}OD$.
查看更多完整答案,请扫码查看


