《2025年全效学习阶段发展评价九年级数学全一册浙教版》

1. 已知抛物线 $ y = ax^{2} + bx + c(a \neq 0) $ 上的部分点的横坐标 $ x $ 与纵坐标 $ y $ 的对应值如下表所示：

下列说法中,正确的是(C)
A.抛物线 $ y = ax^{2} + bx + c $ 的开口向下
B.当 $ x ＜ 3 $ 时,$ y $ 随 $ x $ 的增大而增大
C.方程 $ ax^{2} + bx + c = 0 $ 的根为 $ 0 $ 和 $ 2 $
D.当 $ y ＞ 0 $ 时,$ x $ 的取值范围是 $ 0 ＜ x ＜ 2 $

答案： C

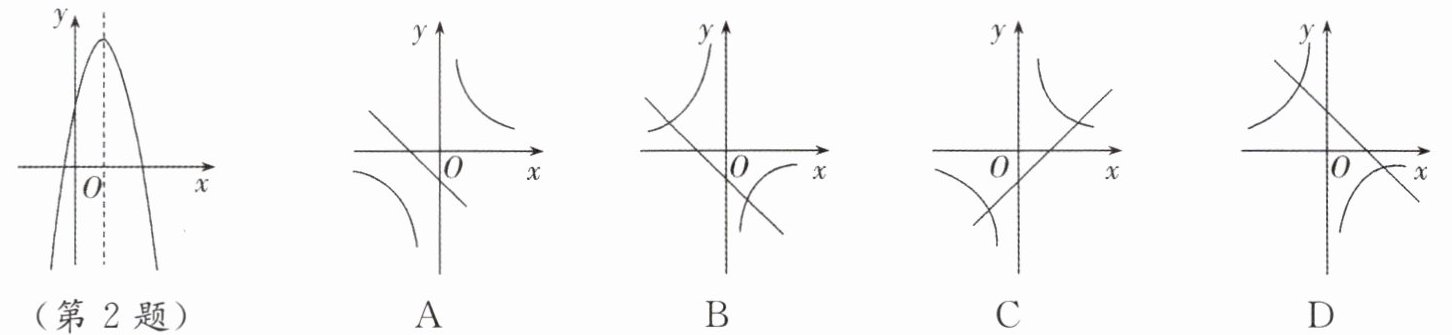
2. 若二次函数 $ y = ax^{2} + bx + c(ac \neq 0) $ 的图象如图所示,则一次函数 $ y = ax + b $ 与反比例函数 $ y = -\frac{c}{x} $ 在同一平面直角坐标系中的大致图象为(D)

答案： D 【解析】由二次函数的图象，得a＜0,b＞0,c＞0.
∵一次函数的表达式为y=ax+b,
∴y随x的增大而减小,且与y轴的交点在y轴的正半轴上.
∵反比例函数的表达式为y=-c/x,-c＜0,
∴反比例函数的图象在第二、四象限.故选D.

3. 已知抛物线 $ y = ax^{2} - 2ax + c(a ＞ 0) $ 过 $ A(-3, y_{1}) $,$ B(-1, y_{2}) $,$ C(2, y_{3}) $,$ D(4, y_{4}) $ 四点,则下列说法中,正确的是(C)
A.若 $ y_{1}y_{2} ＞ 0 $,则 $ y_{3}y_{4} ＞ 0 $
B.若 $ y_{1}y_{4} ＞ 0 $,则 $ y_{2}y_{3} ＞ 0 $
C.若 $ y_{2}y_{4} ＜ 0 $,则 $ y_{1}y_{3} ＜ 0 $
D.若 $ y_{3}y_{4} ＜ 0 $,则 $ y_{1}y_{2} ＜ 0 $

答案： C 【解析】
∵y=ax²-2ax+c=a(x-1)²-a+c,a＞0,
∴抛物线的对称轴为直线x=1,且开口向上，
∴抛物线上越接近对称轴的点,纵坐标越小,
∴y₃＜y₂＜y₄＜y₁.若y₃＜0＜y₂＜y₄＜y₁,则A,B,D的条件成立,结论不成立,故A,B，D均错误；若y₂y₄＜0,则一定有y₃＜y₂＜0＜y₄＜y₁,
∴y₁y₃＜0,故C正确.

4. 已知二次函数 $ y = -x^{2} + 6x - 5 $。
(1) 求二次函数图象的顶点坐标。
(2) 当 $ 1 \leq x \leq 4 $ 时,函数的最大值和最小值分别为多少？

答案： 解:
(1)
∵y=-x²+6x-5=-(x-3)²+4,
∴顶点坐标为(3,4).
(2)
∵顶点坐标为(3,4),
∴当x=3时,y最大=4.当x=1时,y=0；当x=4时,y=3,
∴当1≤x≤4时,函数的最大值为4,最小值为0.

5. 将抛物线 $ y = 2(x - 4)^{2} - 1 $ 先向左平移 $ 4 $ 个单位,再向上平移 $ 2 $ 个单位,平移后所得抛物线的函数表达式为(A)
A.$ y = 2x^{2} + 1 $
B.$ y = 2x^{2} - 3 $
C.$ y = 2(x - 8)^{2} + 1 $
D.$ y = 2(x - 8)^{2} - 3 $

答案： A

6. 设抛物线 $ y = x^{2} + (a + 1)x + a $,其中 $ a $ 为实数。
(1) 若抛物线经过点 $ (-1, m) $,则 $ m = $0。
(2) 将该抛物线向上平移 $ 2 $ 个单位,所得抛物线顶点的纵坐标的最大值为2。

答案：
(1)0
(2)2 【解析】
(1)将点(-1,m)的坐标代入y=x²+(a+1)x+a,得(-1)²+(a+1)×(-1)+a=m,解得m=0.
(2)平移后的抛物线为y=x²+(a+1)x+a+2=(x+(a+1)/2)²-1/4(a-1)²+2,
∴抛物线顶点的纵坐标n=-1/4(a-1)²+2.
∵-1/4＜0,
∴n的最大值为2.