1. 《孙子算经》是中国古代重要的数学著作,其中有一首歌谣:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”意思是:有一根竹竿不知道有多长,量出它在太阳下的影长为一丈五尺,同时立一根长为一尺五寸的标杆,它的影长为五寸,问竹竿有多长(注:1 丈= 10 尺,1 尺= 10 寸)?竹竿的长为(
A.五丈
B.四丈五尺
C.一丈
D.五尺
B
)A.五丈
B.四丈五尺
C.一丈
D.五尺
答案:
B
2. 如图,为了估算某河的宽度,在河对岸边选定一个目标点 A,在近岸取点 B,C,D,使得 AB⊥BC,CD⊥BC,点 E 在 BC 上,并且点 A,E,D 在同一条直线上. 若测得 BE 长为 40 步,EC 长为 20 步,CD 长为 40 步,则估计河的宽度 AB 大约为(1 m≈2 步)(
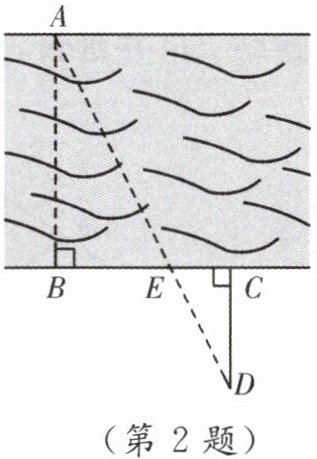
A.80 m
B.40 m
C.8 m
D.4 m
B
)
A.80 m
B.40 m
C.8 m
D.4 m
答案:
B [解析]
∵AB⊥BC,CD⊥BC,
∴AB//CD,
∴△BAE∽△CDE,
∴$\frac{AB}{DC}$=$\frac{BE}{CE}$.
∵BE=40步,CE=20步,DC=40步,
∴$\frac{AB}{40}$=$\frac{40}{20}$,解得AB=80步,约为40m.
∵AB⊥BC,CD⊥BC,
∴AB//CD,
∴△BAE∽△CDE,
∴$\frac{AB}{DC}$=$\frac{BE}{CE}$.
∵BE=40步,CE=20步,DC=40步,
∴$\frac{AB}{40}$=$\frac{40}{20}$,解得AB=80步,约为40m.
3. 《九章算术》中记载了一种测量古井水面以上部分深度的方法. 如图,在井口 A 处立一根垂直于井口的木杆 AB,从木杆的顶端 B 观察井水水岸 D,视线 BD 与井口的直径 AC 相交于点 E. 如果测得 AB= 1 m,AC= 1.6 m,AE= 0.4 m,那么 CD=
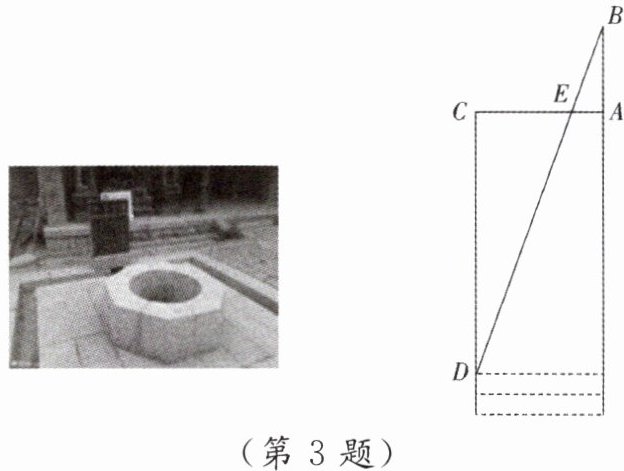
3
m.
答案:
3 [解析]由题意,得AB//CD,
∴△ABE∽△CDE,
∴$\frac{AB}{CD}$=$\frac{AE}{CE}$,即$\frac{1}{CD}$=$\frac{0.4}{1.6−0.4}$,解得CD=3m.
∴△ABE∽△CDE,
∴$\frac{AB}{CD}$=$\frac{AE}{CE}$,即$\frac{1}{CD}$=$\frac{0.4}{1.6−0.4}$,解得CD=3m.
4. 周末,小华和小亮想用所学的数学知识测量家门前小河的宽. 测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点 A,在他们所在的岸边选择了点 B,使得 AB 与河岸垂直,并在点 B 处竖起标杆 BC,再在 AB 的延长线上选择点 D,竖起标杆 DE,使得点 E 与点 C,A 共线. 已知 CB⊥AD 于点 B,ED⊥AD,测得 BC= 1 m,DE= 1.5 m,BD= 8.5 m,示意图如图所示. 请根据相关测量信息,求出河宽 AB.


答案:
解:
∵CB⊥AD,ED⊥AD,
∴CB//ED,
∴△ABC∽△ADE,
∴$\frac{BC}{DE}$=$\frac{AB}{AD}$.
∵BC=1m,DE=1.5m,BD =8.5m,
∴$\frac{1}{1.5}$=$\frac{AB}{AB+8.5}$,解得AB=17m.答:河宽AB为17m.
∵CB⊥AD,ED⊥AD,
∴CB//ED,
∴△ABC∽△ADE,
∴$\frac{BC}{DE}$=$\frac{AB}{AD}$.
∵BC=1m,DE=1.5m,BD =8.5m,
∴$\frac{1}{1.5}$=$\frac{AB}{AB+8.5}$,解得AB=17m.答:河宽AB为17m.
查看更多完整答案,请扫码查看


