《2025年全效学习阶段发展评价九年级数学全一册浙教版》

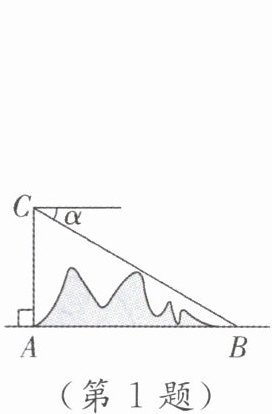
1. 如图,某地修建高速公路,要从A地向B地修一条隧道(点A,B在同一水平面上). 为了测量A,B两地之间的距离,一架直升机从A地出发,垂直上升800m到达C处,在C处观察B地的俯角为α,则A,B两地之间的距离为(D)

A.$800\sin\alpha$m
B.$800\tan\alpha$m
C.$\frac{800}{\sin\alpha}$m
D.$\frac{800}{\tan\alpha}$m

答案： D

2. [教材P23例5改编]如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东45°方向上的B处,此时B处与灯塔P的距离为25$\sqrt{6}$海里(结果保留根号).

答案： 25$\sqrt{6}$

3. 如图,从楼顶A处看楼下荷塘C处的俯角为45°,看楼下荷塘D处的俯角为60°. 已知楼高AB为30m,则荷塘的宽CD为30 - 10$\sqrt{3}$m(结果保留根号).

答案： 30 - 10$\sqrt{3}$

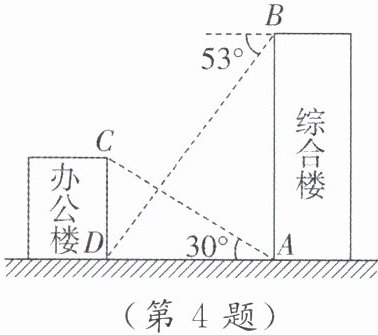
4. 在一次数学课外实践活动中,小明所在的学习小组从如图所示的综合楼顶部B处测得办公楼底部D处的俯角是53°,从综合楼底部A处测得办公楼顶部C处的仰角是30°. 已知综合楼高24m,求办公楼的高度(精确到0.1m；参考数据：$\tan37°\approx0.75$,$\tan53°\approx1.33$,$\sqrt{3}\approx1.73$).

答案： 解:由题意,得AB = 24m,易知∠BDA = 53°,
∴在Rt△ABD中,AD = $\frac{AB}{tan\angle BDA}$≈18.05m.
在Rt△ACD中,∠CAD = 30°,
∴CD = AD·tan∠CAD≈10.4m.
答:办公楼的高度约为10.4m.

5. 如图,小敏、小亮从A,B两地观测空中C处的一个气球,分别测得仰角为30°和60°,A,B两地相距100m. 当气球沿与BA平行的方向飘移10s后到达C'处时,在A处测得气球的仰角为45°.
(1)求气球的高度(精确到0.1m).
(2)求气球飘移的平均速度(精确到0.01m/s).

答案：

(1)如答图,过点C作CD⊥AB于点D.
在Rt△BCD中,∠CBD = 60°,
∴BD = $\frac{CD}{tan\angle CBD}$ = $\frac{\sqrt{3}}{3}$CD.
在Rt△ACD中,∠CAD = 30°,
∴AD = $\frac{CD}{tan\angle CAD}$ = $\sqrt{3}$CD,
∴AB = AD - BD = $\frac{2\sqrt{3}}{3}$CD.
又
∵AB = 100m,
∴CD = 50$\sqrt{3}$≈86.6(m).
答:气球的高度约为86.6m.

(2)如答图,过点C'作C'E⊥AB于点E.
易知四边形C'EDC是矩形,
∴CC' = DE,C'E = CD = 50$\sqrt{3}$m.
在Rt△AC'E中,∠C'AE = 45°,
∴AE = $\frac{C'E}{tan\angle C'AE}$ = 50$\sqrt{3}$m.
由
(1)得AD = $\sqrt{3}$CD = 150m,
∴CC' = DE = AD - AE = 150 - 50$\sqrt{3}$≈63.40(m),
63.40÷10 = 6.34(m/s).
答:气球飘移的平均速度约为6.34m/s.