1. 在$\triangle ABC$中,$a$,$b$,$c分别是\angle A$,$\angle B$,$\angle C$的对边. 若$a^{2}+b^{2}= c^{2}$,则下列说法中,正确的是(
A.$c\cdot \sin A= a$
B.$b\cdot \cos B= c$
C.$a\cdot \tan A= b$
D.$c\cdot \tan B= b$
A
)A.$c\cdot \sin A= a$
B.$b\cdot \cos B= c$
C.$a\cdot \tan A= b$
D.$c\cdot \tan B= b$
答案:
A
2. 如图是教学用的三角尺,已知$AC = 30\mathrm{cm}$,$\angle C = 90^{\circ}$,$\tan \angle BAC= \frac{\sqrt{3}}{3}$,则$BC$的长为(
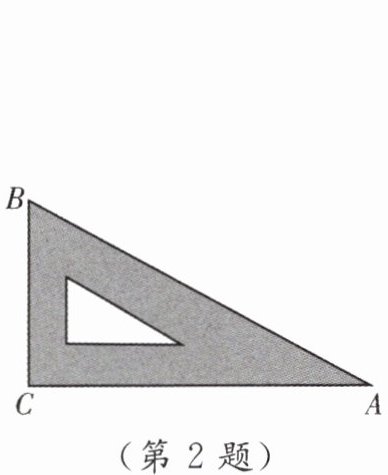
A.$30\sqrt{3}\mathrm{cm}$
B.$20\sqrt{3}\mathrm{cm}$
C.$10\sqrt{3}\mathrm{cm}$
D.$5\sqrt{3}\mathrm{cm}$
C
)
A.$30\sqrt{3}\mathrm{cm}$
B.$20\sqrt{3}\mathrm{cm}$
C.$10\sqrt{3}\mathrm{cm}$
D.$5\sqrt{3}\mathrm{cm}$
答案:
C
3. [教材P19课内练习T2改编]在$\mathrm{Rt}\triangle ABC$中,$a$,$b$,$c分别是\angle A$,$\angle B和\angle C$的对边. 若$\angle C = 90^{\circ}$,$a = 35$,$c = 35\sqrt{2}$,则$\angle A = $
45°
,$b = $35
.
答案:
45° 35
4. 如图,$AB$是伸缩式的遮阳棚,$CD$是窗户,要想在夏至的正午时刻阳光刚好不能射入窗户,则$AB$的长应调整为
]

$\sqrt{3}$
$\mathrm{m}$(假设夏至的正午时刻阳光与地面的夹角为$60^{\circ}$).]

答案:
$\sqrt{3}$
5. [教材P19作业题T1改编]如图,在$\mathrm{Rt}\triangle ABC$中,$\angle C = 90^{\circ}$.
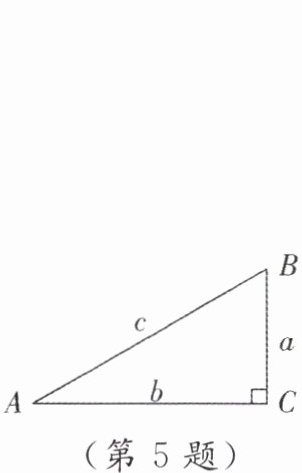
(1)若$c = 12$,$\sin A= \frac{1}{3}$,则$a = $
(2)若$\angle A = 30^{\circ}$,$a = 8$,则$\angle B = $
(3)若$a= \sqrt{15}$,$b= \sqrt{5}$,则$\angle A = $
(4)若$a = 2\sqrt{2}$,$c = 4$,则$\angle A = $

(1)若$c = 12$,$\sin A= \frac{1}{3}$,则$a = $
4
,$b = $$8\sqrt{2}$
.(2)若$\angle A = 30^{\circ}$,$a = 8$,则$\angle B = $
60°
,$c = $16
,$b = $$8\sqrt{3}$
.(3)若$a= \sqrt{15}$,$b= \sqrt{5}$,则$\angle A = $
60°
,$\angle B = $30°
,$c = $$2\sqrt{5}$
.(4)若$a = 2\sqrt{2}$,$c = 4$,则$\angle A = $
45°
,$\angle B = $45°
,$b = $$2\sqrt{2}$
.
答案:
(1)4 $8\sqrt{2}$
(2)60° 16 $8\sqrt{3}$
(3)60° 30° $2\sqrt{5}$
(4)45° 45° $2\sqrt{2}$
(1)4 $8\sqrt{2}$
(2)60° 16 $8\sqrt{3}$
(3)60° 30° $2\sqrt{5}$
(4)45° 45° $2\sqrt{2}$
6. [教材P19作业题T3改编]在$\mathrm{Rt}\triangle ABC$中,$\angle C = 90^{\circ}$. 根据下列条件解直角三角形.
(1)$a = 8$,$\angle B = 60^{\circ}$.
(2)$\angle A = 45^{\circ}$,$b= \sqrt{6}$.
(1)$a = 8$,$\angle B = 60^{\circ}$.
(2)$\angle A = 45^{\circ}$,$b= \sqrt{6}$.
答案:
解:
(1)$\angle A=30^{\circ}$,$c=\frac{a}{\cos B}=16$,$b = a\cdot\tan B=8\sqrt{3}$.
(2)$\angle B=45^{\circ}$,$a=b\cdot\tan A=\sqrt{6}$,$c=\frac{b}{\cos A}=2\sqrt{3}$.
(1)$\angle A=30^{\circ}$,$c=\frac{a}{\cos B}=16$,$b = a\cdot\tan B=8\sqrt{3}$.
(2)$\angle B=45^{\circ}$,$a=b\cdot\tan A=\sqrt{6}$,$c=\frac{b}{\cos A}=2\sqrt{3}$.
查看更多完整答案,请扫码查看


