11. 在平面直角坐标系中,若抛物线 $ y = x^{2} + 2x + k $ 与 $ x $ 轴只有一个交点,则 $ k = $
1
。
答案:
1
12. 已知关于 $ x $ 的一元二次方程 $ x^{2} + x - m = 0 $。
(1) 若方程有两个不相等的实数根,求 $ m $ 的取值范围。
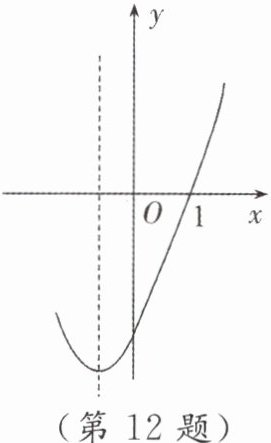
(2) 若二次函数 $ y = x^{2} + x - m $ 的部分图象如图所示,求一元二次方程 $ x^{2} + x - m = 0 $ 的解。
(1) 若方程有两个不相等的实数根,求 $ m $ 的取值范围。
(2) 若二次函数 $ y = x^{2} + x - m $ 的部分图象如图所示,求一元二次方程 $ x^{2} + x - m = 0 $ 的解。

答案:
解:
(1)
∵一元二次方程x²+x-m=0有两个不相等的实数根,
∴Δ>0,即1+4m>0,解得m>-1/4.
(2)易知二次函数y=x²+x-m图象的对称轴为直线x=-1/2,
∴抛物线与x轴的两个交点关于直线x=-1/2对称.由图象得,抛物线与x轴的一个交点坐标为(1,0),
∴另一个交点坐标为(-2,0),
∴一元二次方程x²+x-m=0的解为x₁=1,x₂=-2.
(1)
∵一元二次方程x²+x-m=0有两个不相等的实数根,
∴Δ>0,即1+4m>0,解得m>-1/4.
(2)易知二次函数y=x²+x-m图象的对称轴为直线x=-1/2,
∴抛物线与x轴的两个交点关于直线x=-1/2对称.由图象得,抛物线与x轴的一个交点坐标为(1,0),
∴另一个交点坐标为(-2,0),
∴一元二次方程x²+x-m=0的解为x₁=1,x₂=-2.
13. 如图,桥拱截面 $ OBA $ 可视为抛物线的一部分,在某一时刻,桥拱内的水面宽 $ OA = 8m $,桥拱顶点 $ B $ 到水面的距离为 $ 4m $。
(1) 按如图所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式。
(2) 一艘宽为 $ 1.2m $ 的打捞船径直向桥驶来,当船驶到桥拱下方且距 $ O $ 点 $ 0.4m $ 时,桥下水位刚好在 $ OA $ 处,有一名身高 $ 1.68m $ 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱?请说明理由(假设船底与水面齐平)。
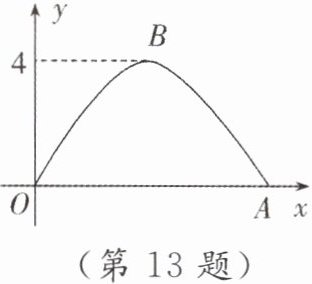
(1) 按如图所示建立平面直角坐标系,求桥拱部分抛物线的函数表达式。
(2) 一艘宽为 $ 1.2m $ 的打捞船径直向桥驶来,当船驶到桥拱下方且距 $ O $ 点 $ 0.4m $ 时,桥下水位刚好在 $ OA $ 处,有一名身高 $ 1.68m $ 的工人站立在打捞船正中间清理垃圾,他的头顶是否会触碰到桥拱?请说明理由(假设船底与水面齐平)。

答案:
解:
(1)
∵水面宽OA=8m,桥拱顶点B到水面的距离为4m,
∴顶点B(4,4).设抛物线的函数表达式为y=a(x-4)²+4,把点O(0,0)的坐标代入,得16a+4=0,解得a=-1/4,
∴抛物线的函数表达式为y=-1/4(x-4)²+4,即y=-1/4x²+2x.
(2)他的头顶不会触碰到桥拱.理由如下:
∵打捞船距O点0.4m,打捞船宽1.2m,工人站立在打捞船正中间,
∴工人距O点0.4+1/2×1.2=1(m).把x=1代入y=-1/4x²+2x,得y=7/4=1.75.
∵1.75>1.68,
∴他的头顶不会触碰到桥拱.
(1)
∵水面宽OA=8m,桥拱顶点B到水面的距离为4m,
∴顶点B(4,4).设抛物线的函数表达式为y=a(x-4)²+4,把点O(0,0)的坐标代入,得16a+4=0,解得a=-1/4,
∴抛物线的函数表达式为y=-1/4(x-4)²+4,即y=-1/4x²+2x.
(2)他的头顶不会触碰到桥拱.理由如下:
∵打捞船距O点0.4m,打捞船宽1.2m,工人站立在打捞船正中间,
∴工人距O点0.4+1/2×1.2=1(m).把x=1代入y=-1/4x²+2x,得y=7/4=1.75.
∵1.75>1.68,
∴他的头顶不会触碰到桥拱.
14. 某景区仅有 $ A $,$ B $ 两个景点,售票处出示的三种购票方式如下表所示:
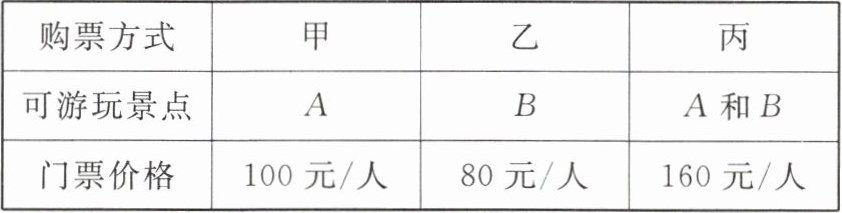
据预测,下个月选择甲、乙、丙三种购票方式的人数分别有 $ 2 $ 万、$ 3 $ 万和 $ 2 $ 万,并且当甲、乙两种门票的价格不变时,丙种门票的价格每下降 $ 1 $ 元,将有 $ 600 $ 人原计划购买甲种门票的游客和 $ 400 $ 人原计划购买乙种门票的游客改为购买丙种门票。
(1) 若丙种门票的价格下降 $ 10 $ 元,求景区下个月的门票总收入。
(2) 当丙种门票的价格下降多少元时,景区下个月的门票总收入有最大值?最大值为多少万元?

据预测,下个月选择甲、乙、丙三种购票方式的人数分别有 $ 2 $ 万、$ 3 $ 万和 $ 2 $ 万,并且当甲、乙两种门票的价格不变时,丙种门票的价格每下降 $ 1 $ 元,将有 $ 600 $ 人原计划购买甲种门票的游客和 $ 400 $ 人原计划购买乙种门票的游客改为购买丙种门票。
(1) 若丙种门票的价格下降 $ 10 $ 元,求景区下个月的门票总收入。
(2) 当丙种门票的价格下降多少元时,景区下个月的门票总收入有最大值?最大值为多少万元?
答案:
解:
(1)由题意,得100×(2-10×0.06)+80×(3-10×0.04)+(160-10)×(2+10×0.06+10×0.04)=798(万元).答:景区下个月的门票总收入为798万元.
(2)设丙种门票的价格降低m元,景区下个月的门票总收入为w万元.由题意,得w=100(2-0.06m)+80(3-0.04m)+(160-m)(2+0.06m+0.04m).化简,得w=-0.1(m-24)²+817.6.
∵-0.1<0,
∴当m=24时,w取最大值,为817.6.答:当丙种门票价格下降24元时,景区下个月的门票总收入有最大值,最大值为817.6万元.
(1)由题意,得100×(2-10×0.06)+80×(3-10×0.04)+(160-10)×(2+10×0.06+10×0.04)=798(万元).答:景区下个月的门票总收入为798万元.
(2)设丙种门票的价格降低m元,景区下个月的门票总收入为w万元.由题意,得w=100(2-0.06m)+80(3-0.04m)+(160-m)(2+0.06m+0.04m).化简,得w=-0.1(m-24)²+817.6.
∵-0.1<0,
∴当m=24时,w取最大值,为817.6.答:当丙种门票价格下降24元时,景区下个月的门票总收入有最大值,最大值为817.6万元.
查看更多完整答案,请扫码查看


