《2025年全效学习阶段发展评价九年级数学全一册浙教版》

7. 已知圆的半径为2cm,圆中的一条弦长为2$\sqrt{3}$cm,则这条弦的中点到弦所对劣弧的中点的距离为(A)
A.1cm
B.2cm
C.$\sqrt{2}$cm
D.$\sqrt{3}$cm

答案： A

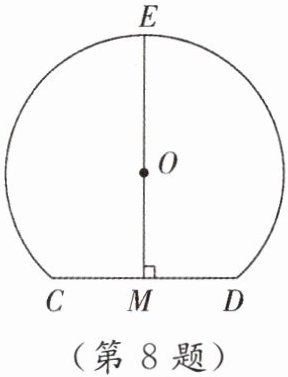
8. 如图,M是CD的中点,EM⊥CD. 若CD= 4,EM= 8,则$\overgroup{CED}$所在的⊙O的半径为$\frac{17}{4}$.

答案： $\frac{17}{4}$

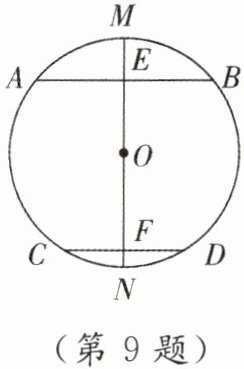
9. 如图,在⊙O中,AB,CD为两条弦,且AB//CD,直径MN经过AB的中点E,交CD于点F. 求证：
(1)F是CD的中点.
(2)$\overgroup{AC}$ = $\overgroup{BD}$.

答案： 证明:
(1)
∵直径MN经过AB的中点E,
∴MN⊥AB.
又
∵AB//CD,
∴MN⊥CD,
∴CF=FD,即F是CD的中点.
(2)
∵MN⊥AB,MN⊥CD,
∴$\widehat{AN}$=$\widehat{BN}$,$\widehat{CN}$=$\widehat{DN}$,
∴$\widehat{AN}$-$\widehat{CN}$=$\widehat{BN}$-$\widehat{DN}$,即$\widehat{AC}$ =$\widehat{BD}$.

10. 如图,隧道的截面由$\overgroup{AED}$和矩形ABCD构成,矩形的长BC为12m,宽AB为3m,隧道的顶端E($\overgroup{AED}$的中点)高出道路(BC)7m.
(1)求$\overgroup{AED}$所在圆的半径.
(2)如果该隧道内设双行道,现有一辆超高货运卡车,车高6.5m,宽2.3m,那么这辆货运卡车能否通过该隧道？

答案：
解:
(1)如答图,设圆心为点O,⊙O的半径为R，连结OE交AD 于点F，连结OA,OD.

易知EF=7−3=4(m),
∴OF=(R−4)m.
由垂径定理的逆定理,得OF垂直平分AD，
∴AF=$\frac{1}{2}$AD=$\frac{1}{2}$BC=6m.
由勾股定理，得AF²+OF²=OA²,
∴6²+(R−4)²=R²,
解得R=6.5,
即$\widehat{AED}$所在圆的半径为6.5m.
(2)如答图,在EF上取一点G,使EG=0.5m,过点G作GH⊥EF,交$\widehat{ED}$于点H,连结OH.
易知OG=OE−EG=6m,OH =6.5m,
∴GH=$\sqrt{OH²−OG²}$=2.5m ＞2.3m,
∴这辆货运卡车能通过该隧道.