《2025年全效学习阶段发展评价九年级数学全一册浙教版》

8. 如图,扇子的圆心角为 $ x $,余下扇形的圆心角为 $ y $,$ x $ 与 $ y $ 的比通常按黄金比来设计,这样的扇子外形比较美观. 若黄金比取 $ 0.618 $,则 $ x $ 约为(138°)

A.$ 222^{\circ} $
B.$ 138^{\circ} $
C.$ 139^{\circ} $
D.$ 108^{\circ} $

答案： B　[解析]　由题意，得$\frac{x}{y}$=0.618,y=360°−x,
∴x=0.618(360°−x),解得x ≈138°.

9. 如图,在 $ \triangle ABC $ 中,$ AB = AC = 4 $,$ BC = 2(\sqrt{5}-1) $,$ \angle A = 36^{\circ} $,$ BD $ 平分 $ \angle ABC $,交 $ AC $ 于点 $ D $. 求证：$ D $ 是线段 $ AC $ 的黄金分割点.

答案： 证明:
∵AB=AC,∠A=36°,
∴∠C=∠ABC=$\frac{180°-∠A}{2}$ =72°.
∵BD平分∠ABC,
∴∠DBC=∠ABD=$\frac{1}{2}$∠ABC =36°,
∴∠A=∠ABD,∠CDB=∠A+∠ABD=72°=∠C,
∴AD=BD=BC=2($\sqrt{5}$−1),
∴$\frac{AD}{AC}$=$\frac{2(\sqrt{5}-1)}{4}$=$\frac{\sqrt{5}-1}{2}$,
∴D是线段AC的黄金分割点.

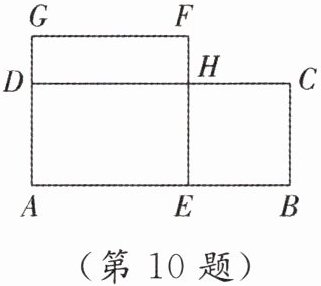
10. [原创]如图,在矩形 $ ABCD $ 中,$ AB＞BC $,在 $ AB $ 上取一点 $ E $,作正方形 $ AEFG $,$ EF $ 与 $ CD $ 相交于点 $ H $. 若 $ S_{\mathrm{正方形}AEFG} = S_{\mathrm{矩形}ABCD} = 4 $,四边形 $ BCHE $ 是正方形,求证：$ H $ 是 $ EF $ 的黄金分割点.

答案： 证明:设BC=x,则BE=EH =x.
∵S正方形AEFG=4,
∴AE=EF =2.
∵S矩形ABCD=4,
∴(2+x)x=4,解得x=$\sqrt{5}$−1(负值舍去),
∴EH=$\sqrt{5}$−1,
∴$\frac{EH}{EF}$=$\frac{\sqrt{5}-1}{2}$,
∴H是EF的黄金分割点.

11. 若一个矩形的短边与长边的比值为 $ \frac{\sqrt{5}-1}{2} $(黄金分割数),我们就把这样的矩形叫做“黄金矩形”.
(1)操作：如图,请在“黄金矩形”$ ABCD(AB＞AD) $ 中,以短边 $ AD $ 为一边作正方形 $ AEFD $(使点 $ E $ 在 $ AB $ 上,点 $ F $ 在 $ CD $ 上).
(2)探究：(1)中得到的四边形 $ EBCF $ 是不是“黄金矩形”？请说明理由.
(3)归纳：通过上述操作及探究,请概括出具有一般性的结论(不需要说明原因).

答案：
解:
(1)如答图，在AB和DC上分别截取AE=DF=AD,连结EF,则四边形AEFD就是所求作的正方形.
(2)四边形EBCF是“黄金矩形”理由如下:设CD=a,AD=BC=b,则$\frac{b}{a}$=$\frac{\sqrt{5}-1}{2}$.
∵四边形AEFD是正方形，
∴DF=AD=b,
∴CF=CD−DF=a−b.易知四边形EBCF是矩形，
∴$\frac{CF}{BC}$=$\frac{a−b}{b}$=$\frac{a}{b}$−1=$\frac{2}{\sqrt{5}-1}$−1=$\frac{\sqrt{5}-1}{2}$,
∴矩形EBCF是“黄金矩形”
(3)在“黄金矩形”内以短边为边作一个正方形后，所得到的另外一个矩形也是“黄金矩形”