《2025年全效学习阶段发展评价九年级数学全一册浙教版》

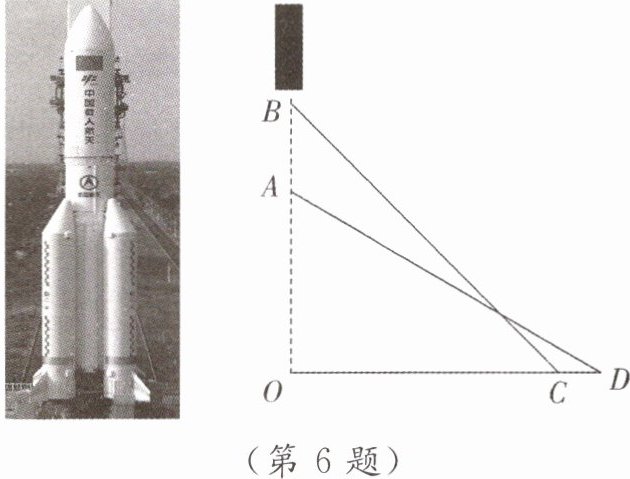
6. “天问一号”探测器在中国文昌航天发射场由长征五号遥四运载火箭发射升空,成功进入预定轨道,开启火星探测之旅,迈出了中国自主开展行星探测的第一步. 如图,运载火箭从地面O处发射,当火箭到达A处时,地面D处的雷达站测得AD= 4000m,仰角为30°,3s后,火箭直线上升到达B处,此时地面C处的雷达站测得B处的仰角为45°,O,C,D在同一直线上. 已知C,D两处相距460m,求火箭从A处到B处的平均速度(精确到1m/s；参考数据：$\sqrt{3}\approx1.732$,$\sqrt{2}\approx1.414$).

答案： 解:设火箭从A处到B处的平均速度为x(m/s),
则AB = 3x(m).
在Rt△ADO中,∠ADO = 30°,AD = 4000m,
∴OA = 2000m,
∴OD = 2000$\sqrt{3}$m.
∵CD = 460m,
∴OC = OD - CD = (2000$\sqrt{3}$ - 460)m.
在Rt△BOC中,∠BCO = 45°,
∴OB = OC = (2000$\sqrt{3}$ - 460)m,
∴AB = OB - OA = (2000$\sqrt{3}$ - 2460)m,
∴3x = 2000$\sqrt{3}$ - 2460,解得x≈335.
答:火箭从A处到B处的平均速度为335m/s.

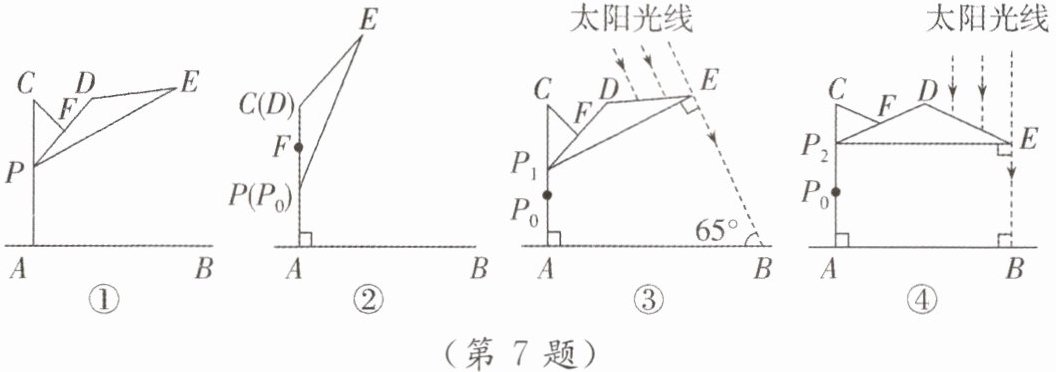
7. 如图①,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC= 2.8m,PD= 2m,CF= 1m,∠DPE= 20°. 当点P位于初始位置P₀时,点D与点C重合(如图②). 根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.
(1)上午10：00时,太阳光线与地面的夹角为65°(如图③),为使遮阳效果最佳,点P需从P₀上调多少距离？
(2)中午12：00时,太阳光线与地面垂直(如图④),为使遮阳效果最佳,点P在(1)的基础上还需上调多少距离？
(精确到0.1m；参考数据：$\sin70°\approx0.94$,$\cos70°\approx0.34$,$\tan70°\approx2.75$,$\sqrt{2}\approx1.41$,$\sqrt{3}\approx1.73$)

答案：

(1)当点P位于初始位置P₀时,CP₀ = 2m.
上午10:00时，太阳光线与地面的夹角为65°,上调的距离为P₀P₁,当P₁E与太阳光线垂直时，遮阳效果最佳.
∵∠BEP₁ = 90°,∠CAB = 90°,∠ABE = 65°,
∴∠AP₁E = 115°,
∴∠CP₁E = 65°.
又
∵∠DP₁E = 20°,
∴∠CP₁F = 45°.
∵CF = P₁F = 1m,
∴∠C = ∠CP₁F = 45°,
∴△CP₁F是等腰直角三角形,
∴P₁C = $\sqrt{2}$m,
∴P₀P₁ = CP₀ - P₁C = 2 - $\sqrt{2}$≈0.6(m).
答:点P需从P₀上调0.6m.
(2)如答图，中午12:00时，太阳光线与地面垂直，上调的距离为P₁P₂,当P₂E与太阳光线垂直时，遮阳效果最佳，过点F作FG⊥AC于点G.

易知P₂E//AB,
∴∠CP₂E = ∠CAB = 90°.
又
∵∠DP₂E = 20°,
∴∠CP₂F = 70°.
易知P₂C = 2CG = 2CF·cos70°≈0.68m.
由
(1)得P₁C = $\sqrt{2}$m,
∴P₁P₂ = P₁C - P₂C = $\sqrt{2}$ - 0.68≈0.7(m).
答:点P在
(1)的基础上还需上调0.7m.