1. 若正多边形的一个内角等于 $120^{\circ}$,则这个多边形的边数是(
A.3
B.6
C.9
D.12
B
)A.3
B.6
C.9
D.12
答案:
B
2. [教材 P100 作业题 T4 改编]如图,在正五边形 $ABCDE$ 中,$\angle CAD$ 的度数为(
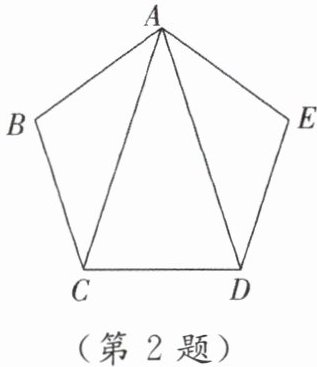
A.$72^{\circ}$
B.$45^{\circ}$
C.$36^{\circ}$
D.$35^{\circ}$
C
)
A.$72^{\circ}$
B.$45^{\circ}$
C.$36^{\circ}$
D.$35^{\circ}$
答案:
C
3. 若正六边形的外接圆半径为 4,则它的边长为(
A.4
B.2
C.$2\sqrt{3}$
D.$4\sqrt{3}$
A
)A.4
B.2
C.$2\sqrt{3}$
D.$4\sqrt{3}$
答案:
A
4. 如图,正六边形 $ABCDEF$ 内接于半径为 4 的圆,则 $B$,$E$ 两点间的距离为

8
.
答案:
8
5. 如图,在正十二边形 $A_1A_2… A_{12}$ 中,连结 $A_3A_7$,$A_7A_{10}$,则 $\angle A_3A_7A_{10}= $______.
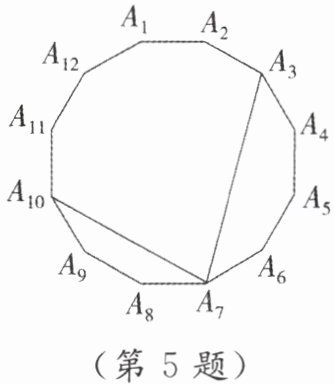

答案:
75° [解析]如答图,作出正十二边形的外接圆⊙O,连结$A_{10}O$ 和$A_{3}O$.

由题意,得$\angle A_{3}OA_{10}=\frac{5}{12}× 360^{\circ}=150^{\circ}$,
∴$\angle A_{3}A_{7}A_{10}=\frac{1}{2}\angle A_{3}OA_{10}=75^{\circ}$.
75° [解析]如答图,作出正十二边形的外接圆⊙O,连结$A_{10}O$ 和$A_{3}O$.

由题意,得$\angle A_{3}OA_{10}=\frac{5}{12}× 360^{\circ}=150^{\circ}$,
∴$\angle A_{3}A_{7}A_{10}=\frac{1}{2}\angle A_{3}OA_{10}=75^{\circ}$.
6. 如图,四边形 $ABCD$ 是 $\odot O$ 的内接正方形,六边形 $AEFCGH$ 是 $\odot O$ 的内接正六边形,连结 $DE$. 求证:$DE$ 是 $\odot O$ 的内接正十二边形的一边.


答案:
证明:如答图,连结$OA$,$OD$,$OE$.

∵四边形$ABCD$是$\odot O$的内接正方形,六边形$AEFCGH$是$\odot O$的内接正六边形,
∴$\angle AOD=90^{\circ}$,$\angle AOE=60^{\circ}$,
∴$\angle DOE=\angle AOD−\angle AOE =30^{\circ}$,
∴$DE$为$\odot O$的内接正十二边形的一边.
证明:如答图,连结$OA$,$OD$,$OE$.

∵四边形$ABCD$是$\odot O$的内接正方形,六边形$AEFCGH$是$\odot O$的内接正六边形,
∴$\angle AOD=90^{\circ}$,$\angle AOE=60^{\circ}$,
∴$\angle DOE=\angle AOD−\angle AOE =30^{\circ}$,
∴$DE$为$\odot O$的内接正十二边形的一边.
7. 如图,在正五边形 $ABCDE$ 中,$F$,$G$ 分别是 $BC$,$CD$ 的中点,$AF$ 与 $BG$ 相交于点 $H$.
(1) 求证:$\triangle ABF\cong\triangle BCG$.
(2) 求 $\angle AHG$ 的度数.

(1) 求证:$\triangle ABF\cong\triangle BCG$.
(2) 求 $\angle AHG$ 的度数.

答案:
(1)证明:
∵五边形$ABCDE$是正五边形,
∴$AB=BC=CD$,$\angle ABF = \angle BCG$.
又
∵$F$,$G$分别是$BC$,$CD$的中点,
∴$BF=CG$.
在$\triangle ABF$和$\triangle BCG$中,
$\because \begin{cases} AB=BC, \\ \angle ABF=\angle BCG, \\ BF=CG, \end{cases}$
∴$\triangle ABF\cong\triangle BCG(SAS)$.
(2)解:
∵$\triangle ABF\cong\triangle BCG$,
∴$\angle GBC=\angle FAB$,
∴$\angle AHG=\angle FAB+\angle ABH=\angle GBC+\angle ABH=\angle ABC$.
易知$\angle ABC=108^{\circ}$,
∴$\angle AHG=108^{\circ}$.
(1)证明:
∵五边形$ABCDE$是正五边形,
∴$AB=BC=CD$,$\angle ABF = \angle BCG$.
又
∵$F$,$G$分别是$BC$,$CD$的中点,
∴$BF=CG$.
在$\triangle ABF$和$\triangle BCG$中,
$\because \begin{cases} AB=BC, \\ \angle ABF=\angle BCG, \\ BF=CG, \end{cases}$
∴$\triangle ABF\cong\triangle BCG(SAS)$.
(2)解:
∵$\triangle ABF\cong\triangle BCG$,
∴$\angle GBC=\angle FAB$,
∴$\angle AHG=\angle FAB+\angle ABH=\angle GBC+\angle ABH=\angle ABC$.
易知$\angle ABC=108^{\circ}$,
∴$\angle AHG=108^{\circ}$.
查看更多完整答案,请扫码查看


