《2025年全效学习阶段发展评价九年级数学全一册浙教版》

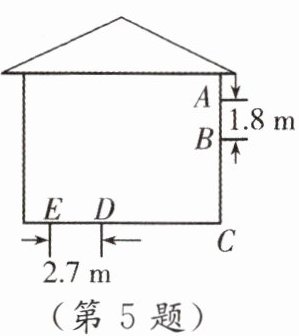
5. 如图,阳光通过窗口 AB 照射到室内,在地面上留下 2.7 m 的亮区 ED,已知亮区到窗口下的墙角的距离 EC= 8.7 m,窗口高 AB= 1.8 m,则窗口底边离地面的高 BC 为(4)

A.4 m
B.3.8 m
C.3.6 m
D.3.4 m

答案： A　　[解析]　如答图，连结AE,BD.易知　AE//BD,
∴　△BCD ∽△ACE,
∴$\frac{AC}{BC}$=$\frac{EC}{DC}$,即$\frac{1.8+BC}{BC}$=$\frac{8.7}{8.7−2.7}$,解得BC=4.

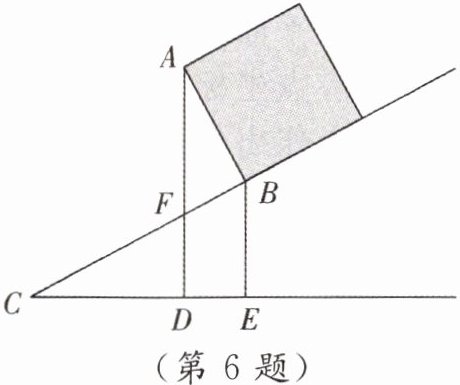
6. [教材 P148 作业题 T2 改编]如图,一只箱子沿着斜面向上运动,箱高 AB= 1.3 m,当 BC= 2.6 m 时,点 B 离地面的距离 BE= 1 m,则此时点 A 离地面的距离为(A)

A.2.2 m
B.2 m
C.1.8 m
D.1.6 m

答案： A　[解析]由题意,得AD//BE,
∴　△CDF∽　△CEB,　∠AFB =∠CBE.又易知∠ABF=∠CEB=90°,
∴△AFB∽△CBE,
∴$\frac{BE}{FB}$=$\frac{BC}{FA}$=$\frac{EC}{BA}$.
∵BC=2.6m,BE=1m,
∴EC=　$\sqrt{BC²−BE²}$=2.4m,
∴$\frac{1}{FB}$=$\frac{2.6}{AF}$=$\frac{2.4}{1.3}$,解得FB=$\frac{13}{24}$,AF=$\frac{169}{120}$.
∵FD//BE,
∴△CDF∽△CEB,
∴$\frac{DF}{EB}$=$\frac{CF}{CB}$,即$\frac{DF}{1}$=$\frac{2.6-\frac{13}{24}}{2.6}$,解得DF=$\frac{19}{24}$,
∴AD=AF+DF=2.2m.

7. 如图,某水平地面上建筑物的高度为 AB,在点 D 和点 F 处分别竖立高为 2 m 的标杆 CD 和 EF,两标杆相隔 52 m,并且建筑物 AB、标杆 CD 和 EF 在同一竖直平面内,从标杆 CD 后退 2 m 到点 G 处,在点 G 处测得建筑物顶端 A 和标杆顶端 C 在同一条直线上. 从标杆 EF 后退 4 m 到点 H 处,在点 H 处测得建筑物顶端 A 和标杆顶端 E 在同一条直线上. 求建筑物的高 AB.

答案： 解:
∵AB⊥BH,CD⊥BH,EF ⊥BH,
∴AB//CD//EF,
∴△CDG∽△ABG,△EFH ∽△ABH,
∴$\frac{CD}{AB}$=$\frac{DG}{BG}$=$\frac{DG}{DG+BD}$,$\frac{EF}{AB}$=$\frac{FH}{BH}$=$\frac{FH}{FH+DF+BD}$.
∵CD=DG=EF=2m,FH=4m,DF=52m,
∴　　$\frac{2}{AB}$　　=　　$\frac{2}{2+BD}$,　　$\frac{2}{AB}$=$\frac{4}{4+52+BD}$,
∴$\frac{2}{2+BD}$=$\frac{4}{4+52+BD}$,解得BD =52,
∴$\frac{2}{AB}$=$\frac{2}{2+52}$,解得AB=54.答:建筑物的高AB为54m.

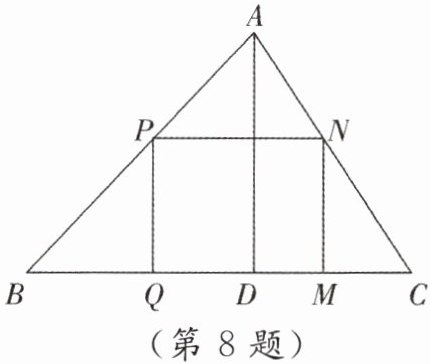
8. [教材 P149 作业题 T5 改编]如图,△ABC 是一块锐角三角形余料,BC= 120 mm,高 AD= 80 mm,要把它加工成矩形零件,使一边在 BC 上,其余两个顶点分别在 AB,AC 上.
(1)求证：△APN∽△ABC.
(2)若这个矩形的长是宽的 2 倍,则宽为多少？

答案：
(1)证明:
∵四边形PNMQ为矩形,
∴BC//PN,
∴△APN∽△ABC.
(2)解:设矩形的宽为x(mm),则长为2x(mm).设AD与PN相交于点E,分两种情况讨论:①PQ为长,PN为宽
∵△APN∽△ABC,
∴$\frac{PN}{BC}$=$\frac{AE}{AD}$,即$\frac{x}{120}$=$\frac{80−2x}{80}$,解得x=30.②PQ为宽,PN为长.
∵△APN∽△ABC,
∴$\frac{PN}{BC}$=$\frac{AE}{AD}$,即$\frac{2x}{120}$=$\frac{80−x}{80}$,解得x=$\frac{240}{7}$.答:矩形的宽为　30　mm　或$\frac{240}{7}$mm.

9. 《九章算术》是我国古代数学名著,书中有下列问题：“今有勾五步,股十二步,问勾中容方几何？”其意思是：今有直角三角形,短直角边长为 5 步,长直角边长为 12 步,问该直角三角形能容纳的正方形边长最大是多少步？该问题的答案是$\frac{60}{17}$步.

答案： $\frac{60}{17}$　[解析]设正方形的边长为x 步,分两种情况讨论:①当正方形有两边在直角三角形的直角边上时，如答图①.易证△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{DE}{BC}$,即$\frac{12−x}{12}$=$\frac{x}{5}$,解得x=$\frac{60}{17}$.②当正方形有一边在直角三角形的斜边上时，如答图②.
∵AB=12,BC=5,∠B=90°,
∴AC=13.易证△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{DE}{CB}$,即$\frac{AD}{13}$=$\frac{x}{5}$,
∴AD=$\frac{13}{5}$x.易证△DBG∽△ABC,
∴$\frac{DB}{AB}$=$\frac{DG}{AC}$,即$\frac{DB}{12}$=$\frac{x}{13}$,
∴DB=$\frac{12}{13}$x,
∴AB=AD+DB=$\frac{13}{5}$x+$\frac{12}{13}$x =12,解得x=$\frac{780}{229}$.
∵$\frac{60}{17}$＞$\frac{780}{229}$,
∴正方形的边长为$\frac{60}{17}$步.