《2025年全效学习阶段发展评价九年级数学全一册浙教版》

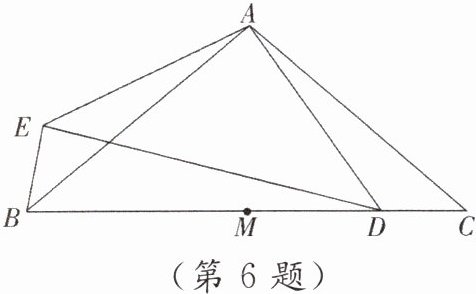
6. [原创]如图,在△ABC中,AB = AC,∠BAC = 100°,M为BC的中点,点D在MC上,以点A为旋转中心,将线段AD顺时针旋转100°得到线段AE,连结BE,DE. 若∠BAD = 85°,则∠BDE = 15°；若BE = 1,DM = 1.5,则BC = 5.

答案： $15^{\circ }$；5

7. 如图,在△ABC中,点D在AB上,CB = CD,将CA绕点C旋转到CE的位置,使得∠ECA = ∠DCB,连结DE,与AC相交于点F,且∠B = 70°,∠A = 10°.
(1)求证：AB = ED.
(2)求∠AFE的度数.

答案：
(1)证明:$\because ∠ECA=∠DCB,$
$\therefore ∠ECA+∠ACD=∠DCB+∠ACD,$
即$∠ECD=∠ACB.$
由旋转的性质,得$CA=CE.$
在$\triangle BCA$和$\triangle DCE$中,
$\because \left\{\begin{array}{l} CB=CD,\\ ∠ACB=∠ECD,\\ CA=CE,\end{array}\right. $
$\therefore \triangle BCA\cong \triangle DCE(SAS),$
$\therefore AB=ED.$
(2)解:$\because CB=CD,$
$\therefore ∠CDB=∠B=70^{\circ }.$
又$\because \triangle BCA\cong \triangle DCE,$
$\therefore ∠CDE=∠B=70^{\circ },$
$\therefore ∠EDA=180^{\circ }-∠CDE-∠CDB=40^{\circ }.$
又$\because ∠A=10^{\circ },$
$\therefore ∠AFE=∠EDA+∠A=50^{\circ }.$

8. 【问题解决】在一节数学课上,老师提出了这样一个问题：如图①,P是正方形ABCD内一点,PA = 1,PB = 2,PC = 3,你能求出∠APB的度数吗？
小明通过观察、思考、分析,形成了如下思路：
思路一,将△PBC绕点B逆时针旋转90°,得到△P'BA,连结P'P,求出∠APB的度数.
思路二,将△APB绕点B顺时针旋转90°,得到△CP'B,连结P'P,求出∠APB的度数.
(1)请参考小明的思路,任选一种写出完整的解答过程.
【类比探究】
(2)如图②,若P是正方形ABCD外一点,PA = 3,PB = 1,PC = √11. 求∠APB的度数.

答案：
解:
(1)如答图①,将$\triangle PBC$绕点B逆时针旋转$90^{\circ }$,得到$\triangle P'BA,$连结$P'P.$
$\because P'B=PB=2,∠P'BP=90^{\circ },$
$\therefore P'P=2\sqrt {2},∠BPP'=45^{\circ }.$
又$\because P'A=PC=3,PA=1,$
$\therefore PA^{2}+P'P^{2}=1+8=9=P'A^{2},$
$\therefore ∠APP'=90^{\circ },$
$\therefore ∠APB=∠APP'+∠BPP'=135^{\circ }.$

(2)如答图②,将$\triangle PBC$绕点B逆时针旋转$90^{\circ }$,得到$\triangle P'BA,$连结$PP'.$
$\because P'B=PB=1,∠P'BP=90^{\circ },$
$\therefore P'P=\sqrt {2},∠BPP'=45^{\circ }.$
又$\because P'A=PC=\sqrt {11},PA=3,$
$\therefore PA^{2}+P'P^{2}=9+2=11=P'A^{2},$
$\therefore ∠APP'=90^{\circ },$
$\therefore ∠APB=∠APP'-∠BPP'=45^{\circ }.$