《2025年全效学习阶段发展评价九年级数学全一册浙教版》

1. 如图,四边形 $ABCD$ 的对角线 $AC$,$BD$ 相交于点 $O$,且将这个四边形分成①②③④四个三角形. 若 $OA:OC = OB:OD$,则下列说法中,正确的是(B)

A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
]

答案： B

2. [教材 $P135$ 课内练习 $T2$ 改编]如图,下列条件中,不能判定 $\triangle ADB \sim \triangle ABC$ 的是(D)

A.$\angle ABD = \angle ACB$
B.$\angle ADB = \angle ABC$
C.$AB^2 = AD \cdot AC$
D.$\frac{AD}{AB} = \frac{AB}{BC}$
]

答案： D

3. 在 $\triangle ABC$ 和 $\triangle A'B'C'$ 中,若 $\angle B = \angle B'$,$AB = 15$,$BC = 9$,$B'C' = 3$,则当 $A'B' = $ 5时,$\triangle ABC \sim \triangle A'B'C'$.

答案： 5

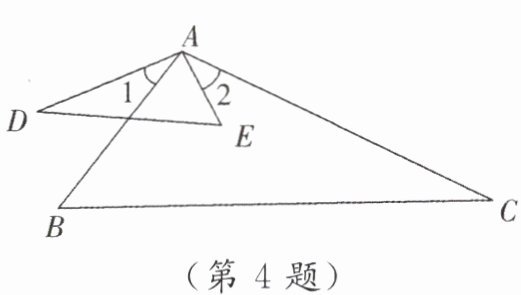
4. 如图,$\angle 1 = \angle 2$,添加一个条件：$\frac{AD}{AC}=\frac{AE}{AB}$(答案不唯一),使得 $\triangle ADE \sim \triangle ACB$.
]

答案： $\frac{AD}{AC}=\frac{AE}{AB}$(答案不唯一)

5. 如图,已知 $\angle BAC = \angle EAD$,$AB = 20.4$,$AC = 48$,$AE = 17$,$AD = 40$. 求证：$\triangle ABC \sim \triangle AED$.
]

答案： 证明:
∵AB=20.4,AC=48,AE =17,AD=40,
∴$\frac{AB}{AE}=\frac{20.4}{17}=1.2$，$\frac{AC}{AD}=\frac{48}{40}=1.2$，
∴$\frac{AB}{AE}=\frac{AC}{AD}$.
　又
∵∠BAC=∠EAD,
∴△ABC∽△AED.

6. 如图,在正方形 $ABCD$ 中,$E$ 为 $AD$ 的中点,点 $F$ 在 $CD$ 上,且 $CF = 3FD$,则 $\triangle ABE$ 与 $\triangle DEF$ 是否相似？请说明理由.
]

答案： 解:△ABE与△DEF相似.理由如下:
∵四边形ABCD为正方形，
∴∠A=∠D=90°,AB=AD =CD.
　设AB=AD=CD=4a.
∵E为AD的中点,CF=3FD,
∴AE=DE=2a,DF=a,
∴$\frac{AB}{DE}=\frac{4a}{2a}=2$，$\frac{AE}{DF}=\frac{2a}{a}=2$，
∴$\frac{AB}{DE}=\frac{AE}{DF}$.
　又
∵∠A=∠D,
∴△ABE∽△DEF.