1. 下列条件中,能确定唯一一个圆的是(
A.以点 $ O $ 为圆心
B.以 $ 2 cm $ 为半径
C.以点 $ O $ 为圆心,$ 5 cm $ 为半径
D.半径为 $ 2 cm $,且经过点 $ A $
C
)A.以点 $ O $ 为圆心
B.以 $ 2 cm $ 为半径
C.以点 $ O $ 为圆心,$ 5 cm $ 为半径
D.半径为 $ 2 cm $,且经过点 $ A $
答案:
C
2. 有下列说法:①直径是弦;②弦是直径;③半圆是弧,弧不一定是半圆;④优弧一定大于劣弧;⑤直径是圆中最长的弦。其中正确的是(
A.①②④
B.①③⑤
C.②③⑤
D.③④⑤
B
)A.①②④
B.①③⑤
C.②③⑤
D.③④⑤
答案:
B
3. 已知 $ \odot O $ 中最长的弦为 $ 8 cm $,则 $ \odot O $ 的半径为(
A.$ 2 cm $
B.$ 4 cm $
C.$ 8 cm $
D.$ 16 cm $
B
)A.$ 2 cm $
B.$ 4 cm $
C.$ 8 cm $
D.$ 16 cm $
答案:
B
4. 已知 $ \odot O $ 的半径为 $ 5 cm $,$ P $ 为 $ \odot O $ 外一点,则 $ OP $ 的长可能是(
A.$ 3 cm $
B.$ 4 cm $
C.$ 5 cm $
D.$ 6 cm $
D
)A.$ 3 cm $
B.$ 4 cm $
C.$ 5 cm $
D.$ 6 cm $
答案:
D
5. 若 $ \odot O $ 的半径为 $ 5 cm $,点 $ A $ 到圆心 $ O $ 的距离 $ OA = 3 cm $,则点 $ A $ 与 $ \odot O $ 的位置关系为(
A.点 $ A $ 在 $ \odot O $ 上
B.点 $ A $ 在 $ \odot O $ 内
C.点 $ A $ 在 $ \odot O $ 外
D.无法确定
B
)A.点 $ A $ 在 $ \odot O $ 上
B.点 $ A $ 在 $ \odot O $ 内
C.点 $ A $ 在 $ \odot O $ 外
D.无法确定
答案:
B
6. 如图,$ MN $ 为 $ \odot O $ 的弦,$ \angle N = 50^{\circ} $,则 $ \angle MON $ 的度数为(
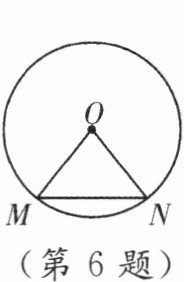
A.$ 40^{\circ} $
B.$ 50^{\circ} $
C.$ 80^{\circ} $
D.$ 100^{\circ} $
C
)
A.$ 40^{\circ} $
B.$ 50^{\circ} $
C.$ 80^{\circ} $
D.$ 100^{\circ} $
答案:
C
7. 如图,在 $ \odot O $ 中,弦是
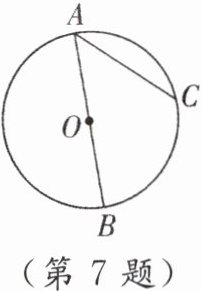
AC,AB
,直径是AB
,优弧是$\overset{\frown}{ABC}$,$\overset{\frown}{CAB}$
,劣弧是$\overset{\frown}{AC}$,$\overset{\frown}{BC}$
。
答案:
AC,AB AB $\overset{\frown}{ABC}$,$\overset{\frown}{CAB}$ $\overset{\frown}{AC}$,$\overset{\frown}{BC}$
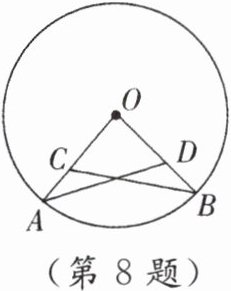
8. 如图,已知 $ OA $,$ OB $ 是 $ \odot O $ 的两条半径,$ C $,$ D $ 为 $ OA $,$ OB $ 上的两点,且 $ AC = BD $。求证:$ AD = BC $。

答案:
证明:
∵OA,OB是$\odot O$的两条半径,
∴OA=OB.
又
∵AC=BD,
∴OC=OD.
在$\triangle OCB$和$\triangle ODA$中,
$\because \left\{\begin{array}{l} OB=OA,\\ \angle O=\angle O,\\ OC=OD,\end{array}\right.$
$\therefore \triangle OCB\cong \triangle ODA(SAS)$,$\therefore AD =BC$.
∵OA,OB是$\odot O$的两条半径,
∴OA=OB.
又
∵AC=BD,
∴OC=OD.
在$\triangle OCB$和$\triangle ODA$中,
$\because \left\{\begin{array}{l} OB=OA,\\ \angle O=\angle O,\\ OC=OD,\end{array}\right.$
$\therefore \triangle OCB\cong \triangle ODA(SAS)$,$\therefore AD =BC$.
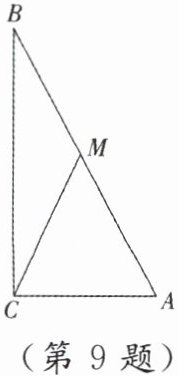
9. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ AC = 2 cm $,$ BC = 4 cm $,$ CM $ 是中线,以点 $ C $ 为圆心,$ \sqrt{5} cm $ 为半径画圆,则点 $ A $,$ B $,$ M $ 与 $ \odot C $ 的位置关系如何?

答案:
解:$\because \angle ACB=90^{\circ }$,$AC=2\ cm$,$BC=4\ cm$,
∴由勾股定理,得$AB=\sqrt {AC^{2}+BC^{2}}=2\sqrt {5}\ cm$.
又
∵CM是中线,
$\therefore CM=\frac {1}{2}AB=\sqrt {5}\ cm$.
$\because AC=2\ cm<\sqrt {5}\ cm$,
∴点A在$\odot C$内.
$\because BC=4\ cm>\sqrt {5}\ cm$,
∴点B在$\odot C$外.
$\because CM=\sqrt {5}\ cm$,
∴点M在$\odot C$上.
∴由勾股定理,得$AB=\sqrt {AC^{2}+BC^{2}}=2\sqrt {5}\ cm$.
又
∵CM是中线,
$\therefore CM=\frac {1}{2}AB=\sqrt {5}\ cm$.
$\because AC=2\ cm<\sqrt {5}\ cm$,
∴点A在$\odot C$内.
$\because BC=4\ cm>\sqrt {5}\ cm$,
∴点B在$\odot C$外.
$\because CM=\sqrt {5}\ cm$,
∴点M在$\odot C$上.
查看更多完整答案,请扫码查看


