10. [原创]有下列说法:①长度相等的两条圆弧是等弧;②能重合的两条圆弧是等弧;③圆的一条直径的两个端点把圆分成两条弧,这两条弧既是优弧,又是劣弧;④在同一平面内,圆心不变,半径变就产生同心圆。其中正确的是(
A.①②
B.③④
C.①③
D.②④
D
)A.①②
B.③④
C.①③
D.②④
答案:
D
11. 如图,点 $ A $,$ B $,$ C $ 都在 $ \odot O $ 上,$ OC \perp OB $,点 $ A $ 在劣弧 $ BC $ 上,且 $ OA = AB $,则 $ \angle ABC = $
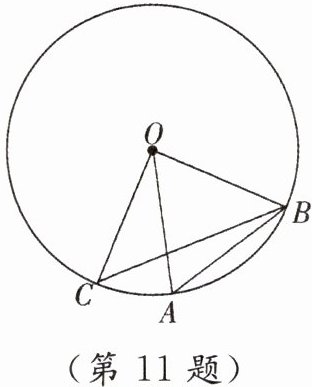
$15^{\circ }$
。
答案:
$15^{\circ }$ 【解析】$\because OC\perp OB$,$OB=OC$,
$\therefore \angle CBO=45^{\circ }$.
$\because OB=OA=AB$,
∴$\triangle OAB$是等边三角形,$\therefore \angle ABO=60^{\circ }$,
$\therefore \angle ABC=\angle ABO-\angle CBO=15^{\circ }$.
$\therefore \angle CBO=45^{\circ }$.
$\because OB=OA=AB$,
∴$\triangle OAB$是等边三角形,$\therefore \angle ABO=60^{\circ }$,
$\therefore \angle ABC=\angle ABO-\angle CBO=15^{\circ }$.
12. 如图,已知 $ \triangle ABC $,$ AB = 5 $,$ BC = 4 $,$ \angle C = 90^{\circ} $,以点 $ C $ 为圆心作 $ \odot C $,半径为 $ r $。当点 $ A $ 在 $ \odot C $ 内,点 $ B $ 在 $ \odot C $ 外时,$ r $ 的取值范围是
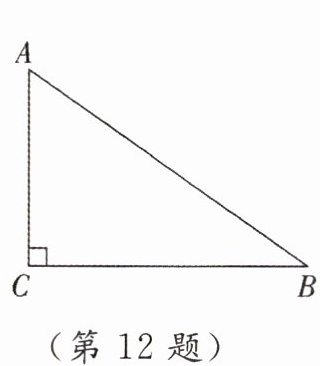
$3< r<4$
。
答案:
$3< r<4$
13. 如图,$ BD $,$ CE $ 是 $ \triangle ABC $ 的高线,$ M $ 为 $ BC $ 的中点。试说明点 $ B $,$ C $,$ D $,$ E $ 在以点 $ M $ 为圆心的同一个圆上。


答案:
证明:如答图,连结ME,MD.

$\because BD$,$CE$是$\triangle ABC$的高线,M为BC的中点,
$\therefore ME=MD=MC=MB=\frac {1}{2}BC$,
∴点B,C,D,E在以点M为圆心的同一个圆上.
证明:如答图,连结ME,MD.

$\because BD$,$CE$是$\triangle ABC$的高线,M为BC的中点,
$\therefore ME=MD=MC=MB=\frac {1}{2}BC$,
∴点B,C,D,E在以点M为圆心的同一个圆上.
14. 如图,线段 $ AD $ 过圆心 $ O $,交 $ \odot O $ 于 $ D $,$ C $ 两点,$ \angle EOD = 78^{\circ} $,$ AE $ 交 $ \odot O $ 于点 $ B $,且 $ AB = OC $。求 $ \angle A $ 的度数。


答案:
解:如答图,连结OB.

$\because AB=OC$,$OB=OC$,
$\therefore AB=OB$,$\therefore \angle 1=\angle A$.
又$\because OB=OE$,
$\therefore \angle E=\angle 2=\angle 1+\angle A=2\angle A$,
$\therefore \angle EOD=\angle E+\angle A=3\angle A$,
即$3\angle A=78^{\circ }$,
$\therefore \angle A=26^{\circ }$.
解:如答图,连结OB.

$\because AB=OC$,$OB=OC$,
$\therefore AB=OB$,$\therefore \angle 1=\angle A$.
又$\because OB=OE$,
$\therefore \angle E=\angle 2=\angle 1+\angle A=2\angle A$,
$\therefore \angle EOD=\angle E+\angle A=3\angle A$,
即$3\angle A=78^{\circ }$,
$\therefore \angle A=26^{\circ }$.
查看更多完整答案,请扫码查看


