1. 下列说法中,正确的是(
A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心距相等,所对的弦相等
D.弦相等,所对的圆心距相等
B
)A.等弦所对的弧相等
B.等弧所对的弦相等
C.圆心距相等,所对的弦相等
D.弦相等,所对的圆心距相等
答案:
B
2. 如图,在$\odot O$中,$\overset{\LARGE{\frown}}{AB}= \overset{\LARGE{\frown}}{AC}$,$\angle A = 30^{\circ}$,则$\angle B$的度数为(
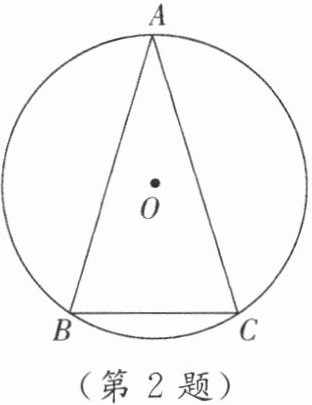
A.$150^{\circ}$
B.$75^{\circ}$
C.$60^{\circ}$
D.$15^{\circ}$
B
)
A.$150^{\circ}$
B.$75^{\circ}$
C.$60^{\circ}$
D.$15^{\circ}$
答案:
B
3. 如图,已知$AB是\odot O$的直径,$C$,$D是\overset{\LARGE{\frown}}{BE}$的三等分点,$\angle AOE = 60^{\circ}$,则$\angle COE$的度数为(
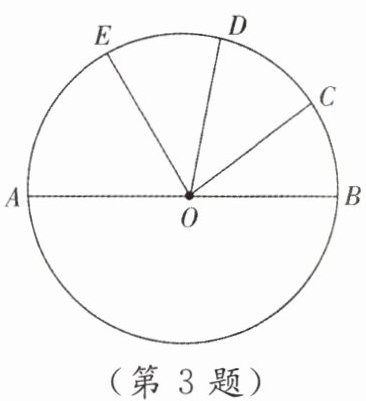
A.$40^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$120^{\circ}$
C
)
A.$40^{\circ}$
B.$60^{\circ}$
C.$80^{\circ}$
D.$120^{\circ}$
答案:
C
4. 如图,圆心角$\angle AOB = 20^{\circ}$,将$\overset{\LARGE{\frown}}{AB}旋转n^{\circ}得到\overset{\LARGE{\frown}}{CD}$,则$\overset{\LARGE{\frown}}{CD}$的度数为
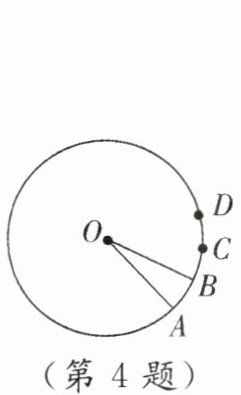
20°
.
答案:
20°
5. 如图,$PO$是直径所在的直线,且$PO平分\angle BPD$,$OE\perp AB$,$OF\perp CD$. 有下列说法:①$AB = CD$;②$\overset{\LARGE{\frown}}{AB}= \overset{\LARGE{\frown}}{CD}$;③$PO = PE$;④$\overset{\LARGE{\frown}}{BG}= \overset{\LARGE{\frown}}{DG}$;⑤$PB = PD$. 其中正确的是
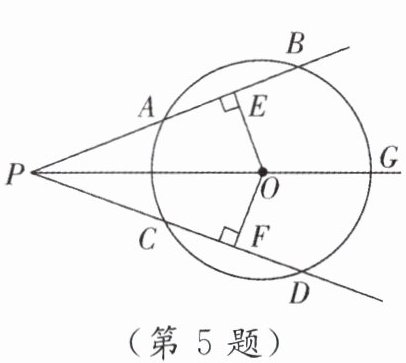
①②④⑤
(填序号).
答案:
①②④⑤
6. 如图,$C$,$D是以线段AB为直径的\odot O$上的两点,且四边形$OBCD$是菱形. 求证:$\overset{\LARGE{\frown}}{AD}= \overset{\LARGE{\frown}}{DC}$.


答案:
证明:如答图,连结OC.
∵四边形OBCD是菱形,
∴OB=BC,∠3=∠2,OD//BC,
∴∠1=∠B.
又
∵OC=OB,
∴OC=BC,
∴∠3=∠B,
∴∠1=∠2,
∴$\overset{\frown}{AD}=\overset{\frown}{DC}$.
∵四边形OBCD是菱形,
∴OB=BC,∠3=∠2,OD//BC,
∴∠1=∠B.
又
∵OC=OB,
∴OC=BC,
∴∠3=∠B,
∴∠1=∠2,
∴$\overset{\frown}{AD}=\overset{\frown}{DC}$.
查看更多完整答案,请扫码查看


