1. 下列说法中,正确的是(
A.过弦的中点的直线平分弦所对的弧
B.过弦的中点的直线必过圆心
C.弦所对的两条弧的中点的连线垂直平分弦,且过圆心
D.与弦垂直的直线平分弦所对的弧
C
)A.过弦的中点的直线平分弦所对的弧
B.过弦的中点的直线必过圆心
C.弦所对的两条弧的中点的连线垂直平分弦,且过圆心
D.与弦垂直的直线平分弦所对的弧
答案:
C
2. 如图,⊙O的弦AB= 8,M是AB的中点,且OM= 3,则⊙O的半径为(
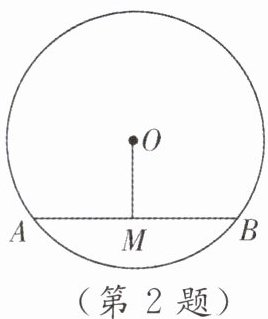
A.8
B.2
C.10
D.5
D
)
A.8
B.2
C.10
D.5
答案:
D
3. [原创]根据图形回答下列问题:
(1)若AC= BC,MN为直径,AB不是直径,则MN⊥
(2)若$\overgroup{AM}$ = $\overgroup{BM}$,MN为直径,则MN⊥
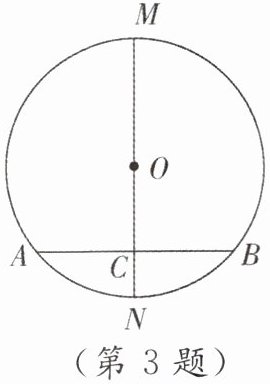
(1)若AC= BC,MN为直径,AB不是直径,则MN⊥
AB
,$\overgroup{AM}$ = $\widehat{BM}$
,$\overgroup{AN}$ = $\widehat{BN}$
.(2)若$\overgroup{AM}$ = $\overgroup{BM}$,MN为直径,则MN⊥
AB
,AC= BC
,$\overgroup{AN}$ = $\widehat{BN}$
.
答案:
(1)AB $\widehat{BM}$ $\widehat{BN}$
(2)AB BC $\widehat{BN}$
(1)AB $\widehat{BM}$ $\widehat{BN}$
(2)AB BC $\widehat{BN}$
4. [教材P79例3改编]已知某桥的跨径为40m,拱高为8m,则该桥的桥拱圆弧的半径为
29m
.
答案:
29m
5. [教材P81作业题T2改编]如图,破残的轮片上,弓形的弦AB为480mm,高CD为70mm. 求这个轮片的直径.
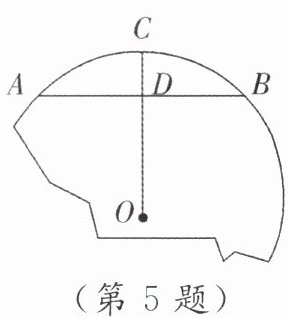

答案:
解:如答图,连结OB.

设轮片的半径为r(mm).
在Rt△OBD中,BD=$\frac{1}{2}$AB=240mm,OB=r(mm),OD=(r−70)mm,OD²+BD²=OB²,
∴(r−70)²+240²=r²,解得r=$\frac{3125}{7}$,
∴2r=$\frac{6250}{7}$.
答:这个轮片的直径为$\frac{6250}{7}$mm.
解:如答图,连结OB.

设轮片的半径为r(mm).
在Rt△OBD中,BD=$\frac{1}{2}$AB=240mm,OB=r(mm),OD=(r−70)mm,OD²+BD²=OB²,
∴(r−70)²+240²=r²,解得r=$\frac{3125}{7}$,
∴2r=$\frac{6250}{7}$.
答:这个轮片的直径为$\frac{6250}{7}$mm.
6. [教材P81作业题T3改编]如图①为一圆柱形零件,其底面为圆,如图②所示.
(1)请用直尺和圆规作出图②的圆心(不写作法,保留作图痕迹).
(2)已知该底面圆的直径为100mm,要在圆柱上铣出宽为28mm的一块平面,如图③所示,问吃刀深度h为多少?
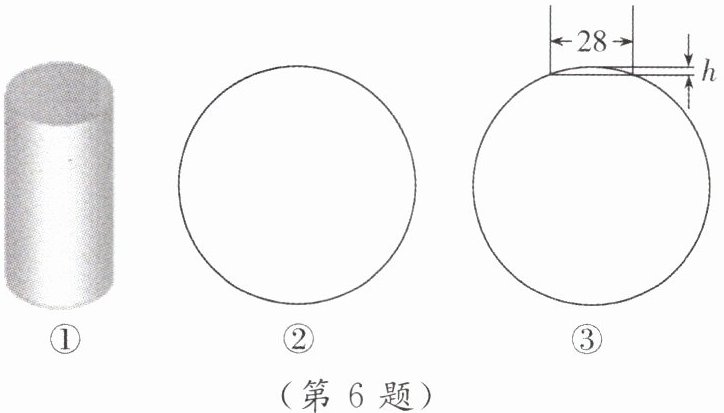
(1)请用直尺和圆规作出图②的圆心(不写作法,保留作图痕迹).
(2)已知该底面圆的直径为100mm,要在圆柱上铣出宽为28mm的一块平面,如图③所示,问吃刀深度h为多少?

答案:
解:
(1)如答图,点O即为所求

(2)由题意,得50²=(50−h)²+14²,解得h₁=2,h₂=98(不合题意,舍去),
∴吃刀深度h为2mm.
解:
(1)如答图,点O即为所求

(2)由题意,得50²=(50−h)²+14²,解得h₁=2,h₂=98(不合题意,舍去),
∴吃刀深度h为2mm.
查看更多完整答案,请扫码查看


