《2025年全效学习阶段发展评价九年级数学全一册浙教版》

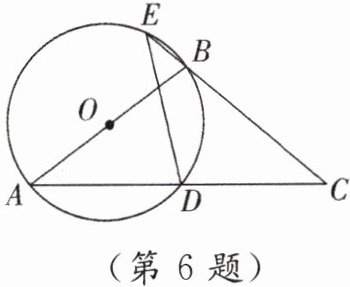
6. 如图,$D是等腰三角形ABC$底边的中点,过点$A$,$B$,$D作\odot O$.
(1)求证：$AB是\odot O$的直径.
(2)延长$CB交\odot O于点E$,连结$DE$,求证：$DC = DE$.

答案：

(1)证明：如答图，连结BD.　　　
∵BA = BC，AD = DC，
∴BD ⊥AC，
∴∠ADB = 90°，
∴AB是⊙O的直径.
(2)
∵BA = BC，
∴∠A = ∠C.又
∵∠A = ∠E，
∴∠C = ∠E，
∴DC = DE.

7. 如图,$A$,$P$,$B$,$C$是圆上的四个点,$\angle APC = \angle BPC = 60^{\circ}$,$AP$,$CB的延长线相交于点D$.
(1)求证：$\triangle ABC$是等边三角形.
(2)若$\angle PAC = 90^{\circ}$,$AB = 2\sqrt{3}$,求$PD$的长.

答案：
(1)证明：
∵∠APC = ∠BPC = 60°，∠APC = ∠ABC，∠BPC = ∠BAC，
∴∠ABC = ∠BAC = 60°，
∴△ABC是等边三角形.
(2)解：
∵∠PAC = 90°，
∴PC是圆的直径，
∴∠PBC = 90°，
∴∠PBD = 90°.
∵△ABC是等边三角形，
∴AC = BC = AB = 2$\sqrt{3}$
∵∠BPC = 60°，
∴∠BCP = 30°，
∴PC = 2PB.
∵PB² + BC² = PC²，
∴PB² + (2$\sqrt{3}$)² = (2PB)²，
∴PB = 2.
∵∠DPB = 180°−∠APC−∠BPC = 60°，
∴∠D = 30°，
∴PD = 2PB = 4.

8. 阅读材料,并回答下列问题：
阿基米德折弦定理：如图①,$AB和BC是\odot O$的两条弦(即折线$ABC$是圆的一条折弦),$BC＞AB$,$M是\overset{\frown}{ABC}$的中点,则从点$M向BC所作垂线的垂足D是折弦ABC$的中点,即$CD = AB + BD$.

下面是运用“截长法”证明$CD = AB + BD$的部分证明过程.
证明：如图②,在$CB上截取CG = AB$,连结$MA$,$MB$,$MC和MG$.
$\because M是\overset{\frown}{ABC}$的中点,$\therefore MA = MC……$
(1)请按照上述证明思路,写出该证明的剩余部分.
(2)如图③,已知等边三角形$ABC内接于\odot O$,$AB = 2$,$D为\overset{\frown}{AC}$上一点,$\angle ABD = 45^{\circ}$,$AE\perp BD于点E$,求$\triangle BDC$的周长.

答案：
(1)证明：在△MBA和△MGC中，
∵$\left\{\begin{array}{l} AB = CG,\\ ∠A = ∠C,\\ MA = MC,\end{array}\right. $
∴△MBA≌△MGC(SAS)，
∴MB = MG.又
∵MD⊥BC，
∴BD = GD，
∴CD = CG + GD = AB + BD.
(2)解：
∵△ABC是等边三角形，
∴AC = BC = AB = 2，
∴$\overset{\frown}{AB}=\overset{\frown}{AC}$，即A为$\overset{\frown}{BAC}$的中点，
∴由阿基米德折弦定理，得ED + DC = BE，即BD + DC = 2BE.
∵AE⊥BD，∠ABD = 45°，
∴△ABE是等腰直角三角形，
∴BE = $\frac{\sqrt{2}}{2}$AB = $\sqrt{2}$，
∴BD + DC = 2$\sqrt{2}$，
∴△BDC的周长为BD + DC + BC = 2$\sqrt{2}$ + 2.