《2025年全效学习阶段发展评价九年级数学全一册浙教版》

7. 已知抛物线的函数表达式为 $ y = 3(x - 2)^2 + 1 $,若将 $ x $ 轴向上平移 2 个单位,将 $ y $ 轴向左平移 3 个单位,则该抛物线在新的平面直角坐标系中的函数表达式为(C)
A.$ y = 3(x + 1)^2 + 3 $
B.$ y = 3(x - 5)^2 + 3 $
C.$ y = 3(x - 5)^2 - 1 $
D.$ y = 3(x + 1)^2 - 1 $

答案： C

8. [教材 P15 作业题 T4 改编]已知二次函数 $ y = x^2 + k $ 的图象经过点 $ (-2, 3) $.
(1)求该二次函数的表达式.
(2)如果点 $ (\frac{1}{2}, m) $,$ (n, 3) $ 也在这个函数的图象上,求 $ m $,$ n $ 的值.

答案： 解:
(1)把点$(-2,3)$的坐标代入$y =x^{2}+k$,得$4+k=3$,解得$k=-1$,
∴该二次函数的表达式为$y=x^{2}-1$.
(2)由题意,得$m=(\frac {1}{2})^{2}-1$,$n^{2}-1=3$,
∴$m=-\frac {3}{4}$,$n=\pm 2$.

9. 已知抛物线 $ y = a(x - h)^2(a \neq 0) $,当 $ x = 2 $ 时,抛物线有最高点,此抛物线过点 $ (1, -3) $. 求该抛物线的函数表达式.

答案： 解:
∵当$x=2$时,抛物线$y=a(x -h)^{2}$有最高点，
∴$a＜0$,$h=2$,
∴抛物线的函数表达式为$y=a(x -2)^{2}$.
∵抛物线过点$(1,-3)$,
∴$a(1-2)^{2}=-3$,解得$a=-3$,
∴抛物线的函数表达式为$y=-3(x-2)^{2}$.

10. 把二次函数 $ y = a(x + m)^2 - k(a \neq 0) $ 的图象先向左平移 2 个单位,再向上平移 4 个单位,得到二次函数 $ y = -\frac{1}{2}(x + 1)^2 - 1 $ 的图象.
(1)试确定 $ a $,$ m $,$ k $ 的值.
(2)指出二次函数 $ y = a(x + m)^2 - k(a \neq 0) $ 图象的开口方向、对称轴和顶点坐标.

答案： 解:
(1)把$y=-\frac {1}{2}(x+1)^{2}-1$反方向移到$y=a(x+m)^{2}-k$,即先向右平移2个单位,再向下平移4个单位，得$y=-\frac {1}{2}(x+1-2)^{2}-1-4$,即$y=-\frac {1}{2}(x-1)^{2}-5$,
∴$a=-\frac {1}{2}$,$m=-1$,$k=5$.
(2)此二次函数图象的开口向下,对称轴为直线$x=1$,顶点坐标为$(1,-5)$.

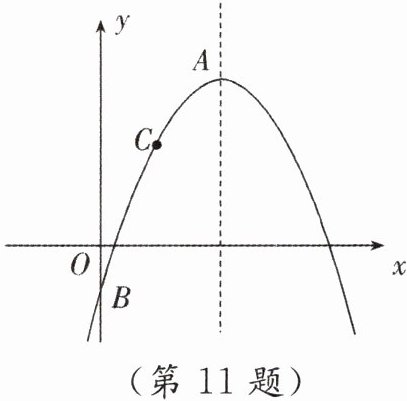
11. 如图,在平面直角坐标系中,已知二次函数 $ y = -\frac{1}{2}(x - m)^2 + 4 $ 图象的顶点为 $ A $,与 $ y $ 轴相交于点 $ B $,异于顶点 $ A $ 的点 $ C(1, n) $ 在该函数图象上.
(1)当 $ m = 5 $ 时,求 $ n $ 的值.
(2)当 $ n = 2 $ 时,若点 $ A $ 在第一象限,结合图象,求当 $ y \geq 2 $ 时,自变量 $ x $ 的取值范围.

答案： 解:
(1)当$m=5$时,$y=-\frac {1}{2}(x-5)^{2}+4$,把$x=1$代入,得$n=-\frac {1}{2}×(1-5)^{2}+4=-4$.
(2)当$n=2$时,把点$C(1,2)$的坐标代入$y=-\frac {1}{2}(x-m)^{2}+4$,得$2=-\frac {1}{2}(1-m)^{2}+4$,解得$m_1=3$,$m_2=-1$(不合题意,舍去).
此时抛物线的对称轴为直线$x =3$.
由抛物线的对称性可知,当$y=2$时,$x=1$或5.
由图象可知,当$y≥2$时,$x$的取值范围是$1≤x≤5$.