《2025年全效学习阶段发展评价九年级数学全一册浙教版》

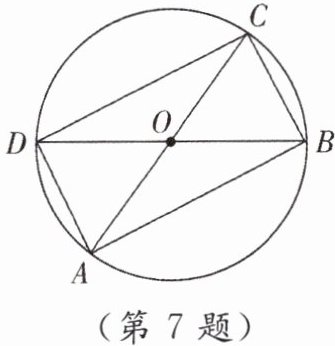
7. [教材P87作业题T5改编]如图,$AC$,$BD是\odot O$的两条直径. 若$\odot O的直径为8$,$\angle AOB = 120^{\circ}$,则四边形$ABCD$的周长为$8+8\sqrt{3}$,面积为$16\sqrt{3}$.

答案： $8+8\sqrt{3}$ $16\sqrt{3}$

8. [教材P86例4改编]如图,以$\triangle ABC的边BC为直径的\odot O分别交AB$,$AC于D$,$E$两点,连结$OD$,$OE$,$DE$.
(1)当$\triangle ABC$为等边三角形时,如图①,判断$\triangle ODE$的形状,并予以证明.
(2)若$\angle A = 60^{\circ}$,$AB\neq AC$,如图②,则(1)中的结论是否仍成立？请说明理由.

答案：
(1)△ODE为等边三角形.证明如下:
∵△ABC为等边三角形,
∴∠B=∠C=60°.
又
∵OB=OD=OE=OC,
∴△OBD,△OEC均为等边三角形,
∴∠BOD=∠COE=60°,
∴∠DOE=60°.
又
∵OD=OE,
∴△ODE为等边三角形.
(2)仍成立.理由如下:
∵∠A+∠B+∠C=180°,
∴∠B+∠C=180°-∠A=120°.
∵OB=OD=OE=OC,
∴∠B=∠BDO,∠C=∠OEC,
∴∠BOD+∠COE=360°-120°×2=120°,
∴∠DOE=60°.
又
∵OD=OE,
∴△ODE为等边三角形.

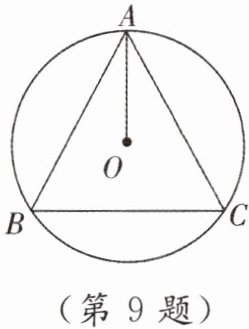
9. [教材P87作业题T6改编]如图,$AB$,$AC是\odot O$的两条弦,且$\overset{\LARGE{\frown}}{AB}= \overset{\LARGE{\frown}}{AC}$.
(1)求证：$AO平分\angle BAC$.
(2)若$AB = 4\sqrt{5}$,$BC = 8$,求半径$OA$的长.

答案：
(1)证明:如答图,连结OB,OC.
∵$\overset{\frown}{AB}=\overset{\frown}{AC}$,
∴AB=AC.
又
∵OB=OC,OA=OA,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO,
即AO平分∠BAC.
(2)解:如答图,延长AO交BC于点E.
∵AB=AC,AO平分∠BAC,
∴AE⊥BC,
∴BE=$\frac{1}{2}$BC=4,
∴AE=$\sqrt{AB^2-BE^2}=8$.
设OA=OB=x.
在Rt△OBE中,OB²=OE²+BE²,
∴x²=(8-x)²+4²,解得x=5,
即半径OA的长为5.

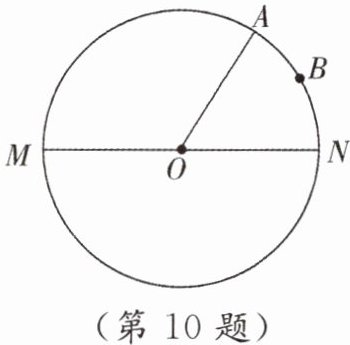
10. 如图,$A是\odot O$上一点,$\angle AON = 60^{\circ}$,$B是\overset{\LARGE{\frown}}{AN}$的中点,$P是直径MN$上的一个动点,$\odot O的半径为1$.
(1)找出当$AP + BP$取最小值时,点$P$的位置.
(2)求出$AP + BP$的最小值.

答案：
(1)如答图,作点A关于MN的对称点A',连结BA'交MN于点P,点P即为所求.
(2)如答图,连结OA',OB.
∵B是$\overset{\frown}{AN}$的中点,
∴∠BON=$\frac{1}{2}$∠AON=30°.
由对称可知,∠A'ON=∠AON=60°,
∴∠BOA'=∠A'ON+∠BON=90°.
又
∵OB=OA'=1,
∴BA'=$\sqrt{2}$,
∴AP+BP的最小值为$\sqrt{2}$.