《2025年全效学习阶段发展评价九年级数学全一册浙教版》

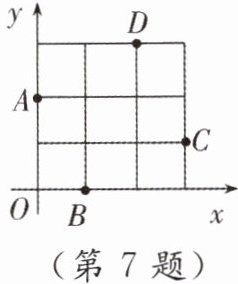
7. 在“探索函数 $ y = ax^{2} + bx + c(a \neq 0) $ 的系数 $ a $,$ b $,$ c $ 与图象的关系”活动中,老师给出了如图所示的平面直角坐标系中的四个点：$ A(0, 2) $,$ B(1, 0) $,$ C(3, 1) $,$ D(2, 3) $。同学们探索了经过这四个点中的三个点的二次函数图象,发现这些图象对应的函数表达式各不相同,其中 $ a $ 的值最大为(A)

A.$ \frac{5}{2} $
B.$ \frac{3}{2} $
C.$ \frac{5}{6} $
D.$ \frac{1}{2} $
]

答案： A 【解析】提示:开口向上且开口越小时,a越大,此时应经过A,B,D三点.

8. 如图,已知经过原点的抛物线 $ y = 2x^{2} + mx $ 与 $ x $ 轴相交于另一点 $ A(2, 0) $。
(1) 求 $ m $ 的值和抛物线的顶点 $ M $ 的坐标。
(2) 求直线 $ AM $ 的函数表达式。
]

答案： 解:
(1)
∵抛物线y=2x²+mx与x轴相交于另一点A(2,0),
∴2×2²+2m=0,
∴m=-4,
∴y=2x²-4x=2(x-1)²-2,
∴顶点M的坐标为(1,-2).
(2)设直线AM的函数表达式为y=kx+b(k≠0).
∵直线AM过点A(2,0),M(1,-2),
∴{2k+b=0,k+b=-2,解得{k=2,b=-4,
∴直线AM的函数表达式为y=2x-4.

9. 已知抛物线 $ y = ax^{2} - 2ax - 8(a \neq 0) $ 经过点 $ (-2, 0) $。
(1) 求抛物线的函数表达式和顶点坐标。
(2) 直线 $ l $ 交抛物线于点 $ A(-4, m) $,$ B(n, 7) $,$ n $ 为正数。若点 $ P $ 在抛物线上且在直线 $ l $ 的下方(不与点 $ A $,$ B $ 重合),分别求出点 $ P $ 的横坐标与纵坐标的取值范围。

答案： 解:
(1)把点(-2,0)的坐标代入y=ax²-2ax-8,得0=4a+4a-8,解得a=1,
∴抛物线的函数表达式为y=x²-2x-8.
∵y=x²-2x-8=(x-1)²-9,
∴抛物线的顶点坐标为(1,-9).
(2)把x=-4代入y=x²-2x-8,得y=(-4)²-2×(-4)-8=16,即m=16.把y=7代入y=x²-2x-8,得7=x²-2x-8,解得n₁=5,n₂=-3.
∵n为正数,
∴n=5,
∴点A的坐标为(-4,16),点B的坐标为(5,7).
∵抛物线开口向上,顶点坐标为(1,-9),
∴抛物线顶点在直线AB下方,
∴-4＜xₚ＜5,-9≤yₚ＜16.

10. 已知二次函数 $ y = ax^{2} + bx + c(a \neq 0) $ 的图象如图所示,有下列说法：① $ abc ＞ 0 $；② $ 4a - 2b + c ＜ 0 $；③ $ a - b \geq x(ax + b) $；④ $ 3a + c ＜ 0 $。其中正确的有(C)

A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个

答案： C 【解析】
∵抛物线开口向下,
∴a＜0.
∵对称轴为直线x=-1,即-b/(2a)=-1,
∴b=2a,
∴b＜0.
∵抛物线与y轴交于正半轴,
∴c＞0,
∴abc＞0,故①正确；
∵抛物线的对称轴为直线x=-1,与x轴的一个交点的横坐标在0和1之间,
∴与x轴的另一个交点的横坐标在-2和-3之间,
∴当x=-2时,y=4a-2b+c＞0,故②错误；
∵当x=-1时,y=ax²+bx+c的最大值为a-b+c,
∴a-b+c≥ax²+bx+c,
∴a-b≥ax²+bx,即a-b≥x(ax+b),故③正确；
∵当x=1时,y=a+b+c＜0,又
∵b=2a,
∴a+2a+c=3a+c＜0,故④正确.故选C.