《2025年全效学习阶段发展评价九年级数学全一册浙教版》

7. 如图,在 $\triangle ABC$ 中,$\angle A = 78°$,$AB = 4$,$AC = 6$. 将 $\triangle ABC$ 沿图示中的虚线剪开,剪下的阴影三角形与原来三角形不相似的是(C)

$\begin{array}{llll}A. & B. & C. & D.\end{array} $

答案： C

8. 在 $\triangle ABC$ 中,$AB = 18\ cm$,$AC = 15\ cm$,$D$ 是 $AB$ 上一点,且 $AD = 6\ cm$,$E$ 是 $AC$ 上一点,当 $AE = $ 5或$\frac{36}{5}$ $cm$,$\triangle ABC$ 与 $\triangle ADE$ 相似.

答案： 5或$\frac{36}{5}$

9. 如图,已知 $AD \cdot AB = AE \cdot AC$,求证：$\triangle FDB \sim \triangle FEC$.
]

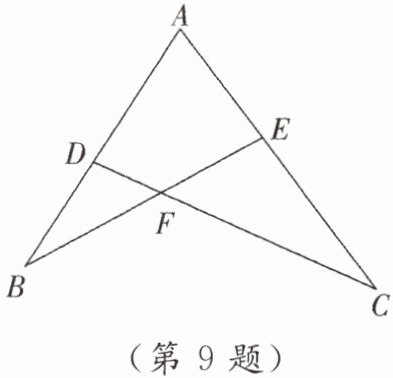
答案： 证明:
∵AD·AB=AE·AC,
∴$\frac{AB}{AC}=\frac{AE}{AD}$.
　又
∵∠A=∠A,
∴△ABE∽△ACD,
∴∠B=∠C.
　又
∵∠BFD=∠CFE,
∴△FDB∽△FEC.

10. 如图,$AC$ 是 $\odot O$ 的直径,弦 $BD$ 交 $AC$ 于点 $E$.
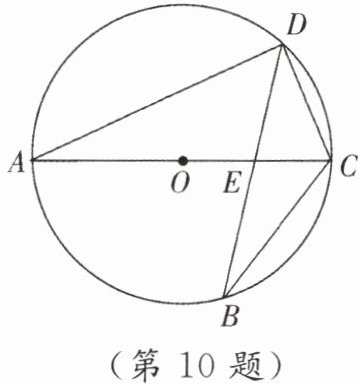
(1) 求证：$\triangle ADE \sim \triangle BCE$.
(2) 若 $AD^2 = AE \cdot AC$,求证：$CD = CB$.
]

答案： 证明:
(1)
∵∠A=∠B,∠AED =∠BEC,
∴△ADE∽△BCE.
(2)
∵AD²=AE·AC,
∴$\frac{AE}{AD}=\frac{AD}{AC}$.
　　又
∵∠A=∠A,
∴△ADE∽△ACD,
∴∠AED=∠ADC;
∵AC是⊙O的直径，
∴∠ADC=90°,
∴∠AED=90°,
∴直径AC⊥BD,
∴$\overset{\frown}{CD}=\overset{\frown}{BC}$,
∴CD=CB.

11. 如图,在 $\triangle ABC$ 中,$AB = AC = 1$,$BC = \frac{\sqrt{5} - 1}{2}$,在 $AC$ 边上截取 $AD = BC$,连结 $BD$.
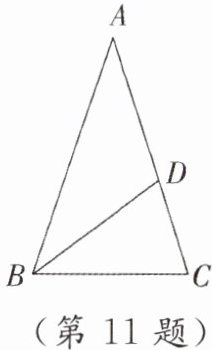
(1) 通过计算,判断 $AD^2$ 与 $AC \cdot CD$ 的大小关系.
(2) 求 $\angle ABD$ 的度数.
]

答案： 解:
(1)
∵AC=1,AD=BC =$\frac{\sqrt{5}-1}{2}$,
∴$AD^{2}=(\frac{\sqrt{5}-1}{2})^{2}=\frac{3-\sqrt{5}}{2}$，
　　CD=AC−AD=$\frac{3-\sqrt{5}}{2}$，
∴AD²=AC·CD.
(2)
∵AD²=AC·CD,
∴BC²=AC·CD,即$\frac{BC}{AC}=\frac{CD}{BC}$.又
∵∠C=∠C,
∴△ABC∽△BDC,
∴$\frac{AB}{BD}=\frac{AC}{BC}$.
∵AB=AC,
∴BD=BC=AD,
∴∠A=∠ABD,∠ABC=∠C =∠BDC;
　　设∠A=∠ABD=x,则∠BDC =∠A+∠ABD=2x,
∴∠ABC=∠C=∠BDC=2x,
∴∠A+∠ABC+∠C=x+2x +2x=180°,
　　解得x=36°,即∠ABD=36°.