《2025年全效学习阶段发展评价九年级数学全一册浙教版》

8. [原创]如图,$\odot M在射线OA$上滚动,$OM的延长线交\odot M于点B$.已知点$M到OA的距离为d$,设$\angle AOM的度数为\alpha$,则$OB$的长为(B)

A.$\left( \dfrac { 1 } { \sin \alpha } - 1 \right) d$
B.$\left( \dfrac { 1 } { \sin \alpha } + 1 \right) d$
C.$( 1 + \sin \alpha ) d$
D.$( 2 - \sin \alpha ) d$

答案： B　[解析]
∵点M到OA的距离为d,∠AOM的度数为α,
∴OM=d/sinα.　由题意得，⊙M与OA相切,
∴MB=d,
∴OB=OM+MB=　(1/sinα +1)d.

9. 如图,正方形$ABCD的边长为1$,以点$A$为圆心,$1为半径的圆与直线BC$的位置关系是相切；以点$A$为圆心,√2/2为半径的圆与直线$BD$相切.

答案： 相切　√2/2　[解析]
∵d=AB=1 =r,
∴以点A为圆心，1为半径的圆与直线BC相切.　易知AO⊥BD,且AO=√2/2,
∴以点A为圆心，√2/2为半径的圆与直线BD相切.

10. 阅读下面的材料,解决最后的问题：
在数学课上,老师请同学思考如下问题：
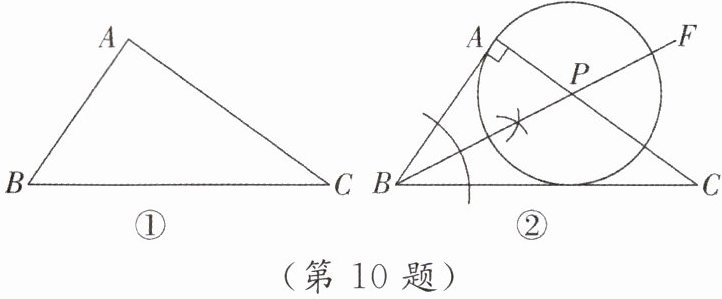
已知：如图①,在$\triangle ABC$中,$\angle A = 90^{\circ}$.
求作：$\odot P$,使得点$P在AC$上,且$\odot P与AB$,$BC$都相切.
小轩的主要作法如图②所示.
先作$\angle ABC的平分线BF$,与$AC相交于点P$；
再以点$P$为圆心,$AP长为半径作\odot P$,
则$\odot P$即为所求.
老师说：“小轩的作法正确.”
求证：$\odot P与BC$相切.

答案：
证明:如答图，过点P作PD⊥BC于点D.　　　　
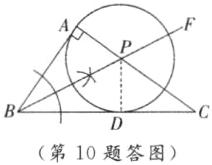
∵BF平分∠ABC,∠A=90°,
∴PA=PD,
∴⊙P与BC相切.

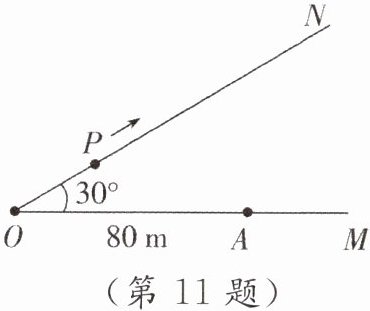
11. 如图,有两条公路$OM$,$ON相交成30^{\circ}$角,沿公路$OM方向离O点80\mathrm{m}处有一所学校A$,当重型运输卡车$P沿道路ON$方向行驶时,在以点$P$为圆心,$50\mathrm{m}$为半径的圆形区域内都会受到卡车噪声的影响,且卡车$P与学校A$的距离越近噪声影响越大,已知重型运输卡车$P沿道路ON方向行驶的速度为18\mathrm{km/h}$.
(1)求对学校$A$的噪声影响最大时,卡车$P与学校A$的距离.
(2)求卡车$P沿道路ON方向行驶一次给学校A$带来噪声影响的时间.

答案：
解:
(1)如答图，过点A作AB⊥ON于点B.
∵∠O=30°,
∴AB=1/2 OA=40m.　　答:对学校A的噪声影响最大时，卡车P与学校A的距离为40m.　　　　　 　　
(2)如答图，以点A为圆心,50m 为半径画弧,交ON于点E,F,分别连结AE,AF,则AE=AF=　　50m,
∴BE=BF=　√(50²−40²)=30 (m),
∴EF=60m.　　18km/h=5m/s,60÷5=12(s).答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12s.