第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
7. 如图所示,在 Rt△ABC 中,∠C= 90°,AC= 10,BC= 5,线段 PQ= AB,P,Q 两点分别在 AC 和过点 A 且垂直于 AC 的射线 AO 上运动,当 AP=
5或10
时,△ABC 和△PQA 全等。
答案:
5或10
8. 如图所示,在△ABC 中,∠C= 90°,AC= BC,AD 平分∠CAB,交 BC 于点 D,DE⊥AB 于点 E。若 AB= 6 cm,则△DBE 的周长为(
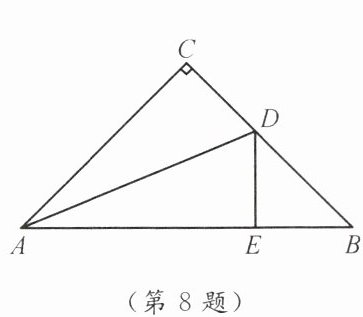
A.6 cm
B.7 cm
C.8 cm
D.9 cm
A
)
A.6 cm
B.7 cm
C.8 cm
D.9 cm
答案:
A
9. 如图,在 Rt△ABC 中,∠C= 90°,BC= 6 cm,AC= 8 cm,按图中所示方法将△BCD 沿 BD 折叠,使点 C 落在 AB 边的点 C'处,那么△ADC'的面积是
6
。
答案:
6
10. 如图,在△ABC 中,P,Q 分别是 BC,AC 上的点,作 PR⊥AB,PS⊥AC,垂足分别是 R,S,PR= PS,AQ= PQ,给出下列结论:①AS= AR。②PQ//AR。③△BRP≌△CSP。其中正确的是______。(填序号)
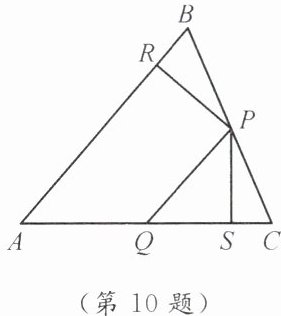

答案:
①②
11. 数学兴趣小组的同学在完成一道数学题:
如图,AC⊥BC,BD⊥AD,AD= BC。求证:BD= AC。
小丽说:“我可以根据全等三角形的判定定理‘AAS’证明两个三角形全等,从而得到 BD= AC。”
小贾说:“我可以根据直角三角形全等的判定定理‘HL’证明两个三角形全等,从而得到 BD= AC。”
小雨说:“我可以根据三角形的面积相等,来证明 BD= AC。”
你认为他们的办法可行吗?并试着证明。
]
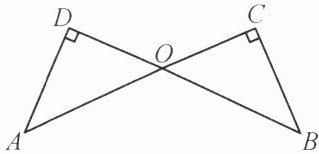
如图,AC⊥BC,BD⊥AD,AD= BC。求证:BD= AC。
小丽说:“我可以根据全等三角形的判定定理‘AAS’证明两个三角形全等,从而得到 BD= AC。”
小贾说:“我可以根据直角三角形全等的判定定理‘HL’证明两个三角形全等,从而得到 BD= AC。”
小雨说:“我可以根据三角形的面积相等,来证明 BD= AC。”
你认为他们的办法可行吗?并试着证明。
]

答案:
小丽、小贾的办法可行,小雨的办法不可行。证明如下:
小丽(AAS):
∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°(垂直定义)。
设AD与BC交于点O,在△AOD和△BOC中:
∠D=∠C(已证),
∠AOD=∠BOC(对顶角相等),
AD=BC(已知),
∴△AOD≌△BOC(AAS)。
∴AO=BO,OD=OC(全等三角形对应边相等)。
∵BD=BO+OD,AC=AO+OC,
∴BD=AC(等量代换)。
小贾(HL):
连接AB,在Rt△ADB和Rt△BCA中:
AB=BA(公共边,斜边),
AD=BC(已知,直角边),
∴Rt△ADB≌Rt△BCA(HL)。
∴BD=AC(全等三角形对应边相等)。
小雨(面积法):
仅“三角形面积相等”无法直接推出BD=AC,缺少面积相等的充分条件(如全等或同底等高),故不可行。
结论: 小丽、小贾的办法可行,小雨的办法不可行。
小丽(AAS):
∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°(垂直定义)。
设AD与BC交于点O,在△AOD和△BOC中:
∠D=∠C(已证),
∠AOD=∠BOC(对顶角相等),
AD=BC(已知),
∴△AOD≌△BOC(AAS)。
∴AO=BO,OD=OC(全等三角形对应边相等)。
∵BD=BO+OD,AC=AO+OC,
∴BD=AC(等量代换)。
小贾(HL):
连接AB,在Rt△ADB和Rt△BCA中:
AB=BA(公共边,斜边),
AD=BC(已知,直角边),
∴Rt△ADB≌Rt△BCA(HL)。
∴BD=AC(全等三角形对应边相等)。
小雨(面积法):
仅“三角形面积相等”无法直接推出BD=AC,缺少面积相等的充分条件(如全等或同底等高),故不可行。
结论: 小丽、小贾的办法可行,小雨的办法不可行。
查看更多完整答案,请扫码查看


