第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
【例1】如图,在$\triangle ABC$中,$AD是BC$边上的高线,$CE是AB$边上的中线,且$DC = BE$,$DG\perp CE于点G$。求证:
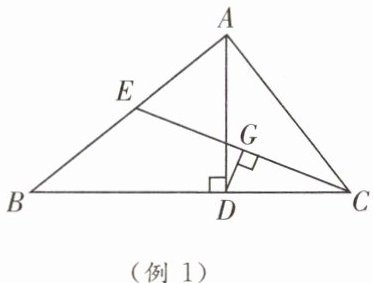
(1)$G是CE$的中点。
(2)$\angle B= 2\angle BCE$。
【分析】(1)连结$DE$,通过证明$\triangle CDE$为等腰三角形,又$DG\perp CE$,继而根据等腰三角形三线合一,证明即可。
(2)由(1)知$DE = BE= DC$,$\angle B= \angle BDE= \angle DEC+\angle DCE$,继而得证。
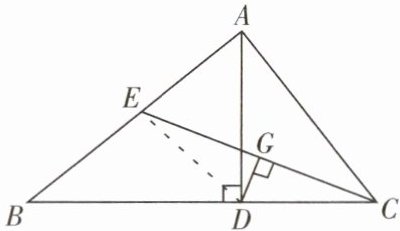
证明:(1)如图,连结$DE$,
因为在$Rt\triangle ABD$中,$E为AB$的中点,
所以$DE = BE$(直角三角形斜边上的中线等于斜边的一半)。
因为$DC = BE$,
所以$DE = DC$。
因为$DG\perp CE于点G$,
所以$G是CE$的中点(等腰三角形三线合一)。
(2)由(1)知$DE = BE= DC$,所以$\angle B= \angle BDE = 2\angle BCE$。

(1)$G是CE$的中点。
(2)$\angle B= 2\angle BCE$。
【分析】(1)连结$DE$,通过证明$\triangle CDE$为等腰三角形,又$DG\perp CE$,继而根据等腰三角形三线合一,证明即可。
(2)由(1)知$DE = BE= DC$,$\angle B= \angle BDE= \angle DEC+\angle DCE$,继而得证。

证明:(1)如图,连结$DE$,
因为在$Rt\triangle ABD$中,$E为AB$的中点,
所以$DE = BE$(直角三角形斜边上的中线等于斜边的一半)。
因为$DC = BE$,
所以$DE = DC$。
因为$DG\perp CE于点G$,
所以$G是CE$的中点(等腰三角形三线合一)。
(2)由(1)知$DE = BE= DC$,所以$\angle B= \angle BDE = 2\angle BCE$。
答案:
证明:
(1)如图,连结$DE$,
因为在$Rt \bigtriangleup ABD$中,$E$为$AB$的中点,
所以$DE = BE$(直角三角形斜边上的中线等于斜边的一半)。
因为$DC = BE$,
所以$DE = DC$。
因为$DG \perp CE$于点$G$,
所以$G$是$CE$的中点(等腰三角形三线合一)。
(2)由(1)知$DE = BE$,所以$\angle B = \angle BDE$。
因为$DE = DC$,所以$\angle DEC = \angle DCE$。
因为$\angle BDE = \angle DEC + \angle DCE$,
所以$\angle B = 2\angle BCE$。
(1)如图,连结$DE$,
因为在$Rt \bigtriangleup ABD$中,$E$为$AB$的中点,
所以$DE = BE$(直角三角形斜边上的中线等于斜边的一半)。
因为$DC = BE$,
所以$DE = DC$。
因为$DG \perp CE$于点$G$,
所以$G$是$CE$的中点(等腰三角形三线合一)。
(2)由(1)知$DE = BE$,所以$\angle B = \angle BDE$。
因为$DE = DC$,所以$\angle DEC = \angle DCE$。
因为$\angle BDE = \angle DEC + \angle DCE$,
所以$\angle B = 2\angle BCE$。
【例2】如图,在四边形$ABCD$中,$AC\perp BD于点E$,$BE = DE$,已知$AC = 10\space cm$,$BD = 8\space cm$,求阴影部分的面积。
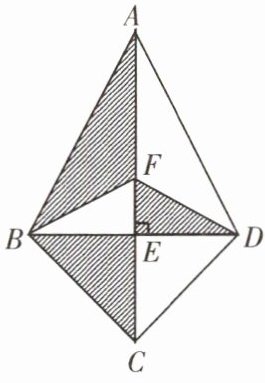
【分析】要求阴影部分的面积,只要将直线$AC右侧的阴影部分沿直线AC$作轴对称变换,则阴影部分的面积即为$\triangle ABC$的面积。
解:由轴对称性得阴影部分的面积$=S_{\triangle ABC}= \frac{1}{2}AC\cdot BE= \frac{1}{2}AC\cdot\frac{BD}{2}= \frac{1}{2}×10×\frac{8}{2}= 20\space(cm^2)$。

【分析】要求阴影部分的面积,只要将直线$AC右侧的阴影部分沿直线AC$作轴对称变换,则阴影部分的面积即为$\triangle ABC$的面积。
解:由轴对称性得阴影部分的面积$=S_{\triangle ABC}= \frac{1}{2}AC\cdot BE= \frac{1}{2}AC\cdot\frac{BD}{2}= \frac{1}{2}×10×\frac{8}{2}= 20\space(cm^2)$。
答案:
解:
∵$AC\perp BD$,$BE = DE$,
由轴对称性可知,阴影部分的面积等于$\triangle ABC$的面积。
∵$AC = 10\space cm$,$BD = 8\space cm$,
∴$S_{\triangle ABC}=\frac{1}{2}AC\cdot BE$
$=\frac{1}{2}AC\cdot\frac{BD}{2}$
$=\frac{1}{2}×10×\frac{8}{2}$
$= 20\space(cm^2)$
即阴影部分的面积为$20\space cm^2$。
∵$AC\perp BD$,$BE = DE$,
由轴对称性可知,阴影部分的面积等于$\triangle ABC$的面积。
∵$AC = 10\space cm$,$BD = 8\space cm$,
∴$S_{\triangle ABC}=\frac{1}{2}AC\cdot BE$
$=\frac{1}{2}AC\cdot\frac{BD}{2}$
$=\frac{1}{2}×10×\frac{8}{2}$
$= 20\space(cm^2)$
即阴影部分的面积为$20\space cm^2$。
【例3】如图,在等边$\triangle ABC$中,$AO是\triangle ABC$的角平分线,$D为AO$上一点,以$CD为一边且在CD下方作等边\triangle CDE$,连结$BE$。
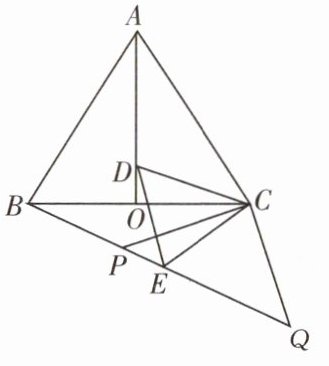
(1)求证:$\triangle ACD\cong\triangle BCE$。
(2)延长$BE至点Q$,$P为BQ$上一点,连结$CP$,$CQ$,使$CP = CQ= 5$。若$BC = 8$,求$PQ$的长。
【分析】(1)由$\triangle ABC与\triangle DCE$是等边三角形,可得$AC = BC$,$DC = EC$,$\angle ACB= \angle DCE = 60^\circ$,又由$\angle ACD+\angle DCB= \angle ECB+\angle DCB = 60^\circ$,即可证得$\angle ACD= \angle BCE$,所以根据$SAS即可证得\triangle ACD\cong\triangle BCE$。
(2)首先过点$C作CH\perp BQ于点H$,由等边三角形的性质,即可求得$\angle DAC = 30^\circ$,由(1)的结论可知$\angle PBC= \angle DAC = 30^\circ$,即可求得$CH= \frac{1}{2}BC$。再根据直角三角形的勾股定理即可求得$PH和QH$的长,最后得到$PQ$的长。
(1)证明:因为$\triangle ABC与\triangle DCE$是等边三角形,
所以$AC = BC$,$DC = EC$,$\angle ACB= \angle DCE = 60^\circ$,
所以$\angle ACD+\angle DCB= \angle ECB+\angle DCB = 60^\circ$,
所以$\angle ACD= \angle BCE$,
所以$\triangle ACD\cong\triangle BCE(SAS)$。
(2)解:如图,过点$C作CH\perp BQ于点H$,

因为$\triangle ABC$是等边三角形,$AO$是角平分线,
所以$\angle DAC = 30^\circ$。
因为$\triangle ACD\cong\triangle BCE$,
所以$\angle PBC= \angle DAC = 30^\circ$,
所以在$Rt\triangle BHC$中,$CH= \frac{1}{2}BC= \frac{1}{2}×8 = 4$。
因为$PC = CQ= 5$,$CH = 4$,
所以$PH = QH= 3$,
所以$PQ = 6$。

(1)求证:$\triangle ACD\cong\triangle BCE$。
(2)延长$BE至点Q$,$P为BQ$上一点,连结$CP$,$CQ$,使$CP = CQ= 5$。若$BC = 8$,求$PQ$的长。
【分析】(1)由$\triangle ABC与\triangle DCE$是等边三角形,可得$AC = BC$,$DC = EC$,$\angle ACB= \angle DCE = 60^\circ$,又由$\angle ACD+\angle DCB= \angle ECB+\angle DCB = 60^\circ$,即可证得$\angle ACD= \angle BCE$,所以根据$SAS即可证得\triangle ACD\cong\triangle BCE$。
(2)首先过点$C作CH\perp BQ于点H$,由等边三角形的性质,即可求得$\angle DAC = 30^\circ$,由(1)的结论可知$\angle PBC= \angle DAC = 30^\circ$,即可求得$CH= \frac{1}{2}BC$。再根据直角三角形的勾股定理即可求得$PH和QH$的长,最后得到$PQ$的长。
(1)证明:因为$\triangle ABC与\triangle DCE$是等边三角形,
所以$AC = BC$,$DC = EC$,$\angle ACB= \angle DCE = 60^\circ$,
所以$\angle ACD+\angle DCB= \angle ECB+\angle DCB = 60^\circ$,
所以$\angle ACD= \angle BCE$,
所以$\triangle ACD\cong\triangle BCE(SAS)$。
(2)解:如图,过点$C作CH\perp BQ于点H$,

因为$\triangle ABC$是等边三角形,$AO$是角平分线,
所以$\angle DAC = 30^\circ$。
因为$\triangle ACD\cong\triangle BCE$,
所以$\angle PBC= \angle DAC = 30^\circ$,
所以在$Rt\triangle BHC$中,$CH= \frac{1}{2}BC= \frac{1}{2}×8 = 4$。
因为$PC = CQ= 5$,$CH = 4$,
所以$PH = QH= 3$,
所以$PQ = 6$。
答案:
(1)证明见上;
(2)6。
(1)证明见上;
(2)6。
查看更多完整答案,请扫码查看


