第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
12. 如图是用10根火柴棒搭成的一个三角形,你能否移动其中的3根,摆出一对全等的三角形?画出你的方案。移动其中4根能否摆出一对全等的三角形?请画图说明,并与同伴交流。


答案:
(1)移动3根火柴棒的方案:
将原三角形顶部的3根火柴棒中的2根分别移到原三角形底边的左侧和右侧,形成两个各有5根火柴棒的小三角形。
这两个小三角形是全等的,每个小三角形都由5根火柴棒组成。
(2)移动4根火柴棒的方案:
将原三角形左侧的3根火柴棒中的2根移到原三角形底边右侧上方,形成两个各有6根火柴棒和4根火柴棒的小三角形。
将原三角形顶部的1根火柴棒移到原三角形底边右侧下方,补全较小的三角形。
这两个小三角形是全等的,一个由6根火柴棒组成,另一个由4根火柴棒组成。
将原三角形顶部的3根火柴棒中的2根分别移到原三角形底边的左侧和右侧,形成两个各有5根火柴棒的小三角形。
这两个小三角形是全等的,每个小三角形都由5根火柴棒组成。
(2)移动4根火柴棒的方案:
将原三角形左侧的3根火柴棒中的2根移到原三角形底边右侧上方,形成两个各有6根火柴棒和4根火柴棒的小三角形。
将原三角形顶部的1根火柴棒移到原三角形底边右侧下方,补全较小的三角形。
这两个小三角形是全等的,一个由6根火柴棒组成,另一个由4根火柴棒组成。
13. 如图所示,△ABE≌△EDC,点E在BD上,AB⊥BD,B为垂足。
(1)AE和CE垂直吗?AE和EC相等吗?
(2)将图中的△ABE绕点E按顺时针方向旋转,分别画出满足下列条件的图形并说出此时△ABE与△EDC中相等的边和角。
①使AE与CE重合。②使AE与CE垂直。③使AE与EC在同一条直线上。

(1)AE和CE垂直吗?AE和EC相等吗?
(2)将图中的△ABE绕点E按顺时针方向旋转,分别画出满足下列条件的图形并说出此时△ABE与△EDC中相等的边和角。
①使AE与CE重合。②使AE与CE垂直。③使AE与EC在同一条直线上。

答案:
(1)因为$\triangle ABE\cong\triangle EDC$,所以$AE=EC$,$\angle AEB=\angle ECD$,$\angle BAE=\angle DEC$。
因为$AB\perp BD$,所以$\angle ABE = 90^\circ$,$\angle BAE+\angle AEB = 90^\circ$。
所以$\angle DEC+\angle ECD = 90^\circ$,$\angle CED = 90^\circ$。
即$AE\perp CE$。
(2)①使$AE$与$CE$重合,$AB=DE$,$BE=CD$,$\angle B=\angle D$,$\angle BAE=\angle CED$,$\angle AEB=\angle ECD$。
②使$AE$与$CE$垂直,$AB=DE$,$BE=CD$,$\angle B=\angle D$,$\angle BAE=\angle CED$,$\angle AEB=\angle ECD$。
③使$AE$与$EC$在同一条直线上,$AB=DE$,$BE=CD$,$\angle B=\angle D$,$\angle BAE=\angle CED$,$\angle AEB=\angle ECD$。
因为$AB\perp BD$,所以$\angle ABE = 90^\circ$,$\angle BAE+\angle AEB = 90^\circ$。
所以$\angle DEC+\angle ECD = 90^\circ$,$\angle CED = 90^\circ$。
即$AE\perp CE$。
(2)①使$AE$与$CE$重合,$AB=DE$,$BE=CD$,$\angle B=\angle D$,$\angle BAE=\angle CED$,$\angle AEB=\angle ECD$。
②使$AE$与$CE$垂直,$AB=DE$,$BE=CD$,$\angle B=\angle D$,$\angle BAE=\angle CED$,$\angle AEB=\angle ECD$。
③使$AE$与$EC$在同一条直线上,$AB=DE$,$BE=CD$,$\angle B=\angle D$,$\angle BAE=\angle CED$,$\angle AEB=\angle ECD$。
14. 如图所示,已知在△ABC中,AB= AC= 10 cm,BC= 8 cm,D为AB的中点,点P在线段BC上以3 cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A以a cm/s的速度运动,设运动的时间为t(s)。
(1)求CP的长。
(2)若以C,P,Q为顶点的三角形和以B,D,P为顶点的三角形全等,且∠B和∠C是对应角,求a的值。
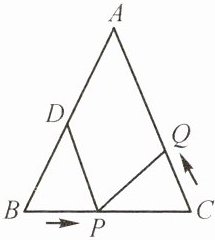
(1)求CP的长。
(2)若以C,P,Q为顶点的三角形和以B,D,P为顶点的三角形全等,且∠B和∠C是对应角,求a的值。

答案:
(1) 由题意,点$P$的速度为$3 cm/s$,运动时间为$t s$,所以$BP = 3t cm$。
因为$BC = 8 cm$,所以$CP = BC - BP = 8 - 3t cm$。
(2) 因为$AB = AC$,所以$\angle B = \angle C$。
分两种情况讨论:
当$BD = CP$时,
因为$D$为$AB$的中点,$AB = 10 cm$,所以$BD = \frac{1}{2}AB = 5 cm$。
则$5 = 8 - 3t$,解得$t = 1$。
因为$\triangle BDP \cong \triangle CPQ$,所以$BP = CQ$,即$3t = at$,$t \neq 0$,所以$a = 3$。
当$BP = CP$时,$3t = 8 - 3t$,解得$t=\frac{4}{3}$。
因为$\triangle BDP \cong \triangle CQP$,所以$BD = CQ$,即$5 = a× \frac{4}{3}$,解得$a = \frac{15}{4}$。
综上所述,$a$的值为$3$或$\frac{15}{4}$。
(1) 由题意,点$P$的速度为$3 cm/s$,运动时间为$t s$,所以$BP = 3t cm$。
因为$BC = 8 cm$,所以$CP = BC - BP = 8 - 3t cm$。
(2) 因为$AB = AC$,所以$\angle B = \angle C$。
分两种情况讨论:
当$BD = CP$时,
因为$D$为$AB$的中点,$AB = 10 cm$,所以$BD = \frac{1}{2}AB = 5 cm$。
则$5 = 8 - 3t$,解得$t = 1$。
因为$\triangle BDP \cong \triangle CPQ$,所以$BP = CQ$,即$3t = at$,$t \neq 0$,所以$a = 3$。
当$BP = CP$时,$3t = 8 - 3t$,解得$t=\frac{4}{3}$。
因为$\triangle BDP \cong \triangle CQP$,所以$BD = CQ$,即$5 = a× \frac{4}{3}$,解得$a = \frac{15}{4}$。
综上所述,$a$的值为$3$或$\frac{15}{4}$。
查看更多完整答案,请扫码查看


