《2025年新课标学习方法指导丛书八年级数学上册浙教版》

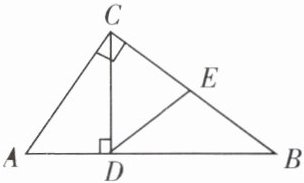
7. 如图,在△ABC 中,∠ACB= 90°,CD⊥AB 于点 D,E 是 BC 的中点,∠A= 55°,求∠DEC 的度数。

答案： $\because \angle ACB=90^{\circ}$，$\angle A=55^{\circ}$，
$\therefore \angle B=90^{\circ}-\angle A=35^{\circ}$。
$\because CD\perp AB$，E是BC的中点，
$\therefore DE=BE=\frac{1}{2}BC$（直角三角形斜边上的中线等于斜边的一半）。
$\therefore \angle BDE=\angle B=35^{\circ}$。
$\therefore \angle DEC=\angle B+\angle BDE=35^{\circ}+35^{\circ}=70^{\circ}$。

8. 如图,在四边形 ABCD 中,∠ABC= ∠ADC= 90°,E 为对角线 AC 的中点,连结 BE,ED,BD。若∠BAD= 58°,则∠EBD 的度数为(A)
A.32°
B.34°
C.36°
D.38°

答案： A

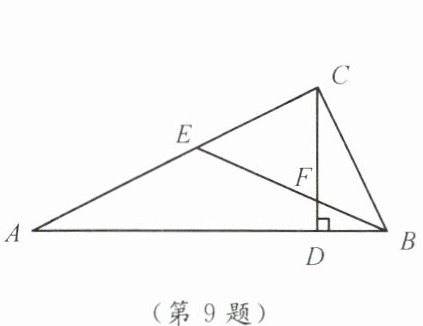
9. 如图,已知△ABC 中,∠ACB= 90°,CD 为 AB 边上的高,∠ABC 的平分线 BE 分别交 CD,CA 于点 F,E,则下列结论正确的有(A)
①∠CFE= ∠CEF。②∠FCB= ∠FBC。③∠A= ∠DCB。④∠CFE 与∠CBF 互余。

A.①③④
B.②③④
C.①②④
D.①②③

答案： A

10. 如图,∠AOP= ∠BOP= 15°,PC//OA,PD⊥OA 于点 D,若 PC= 4,则 PD 的长为2。

答案： 2

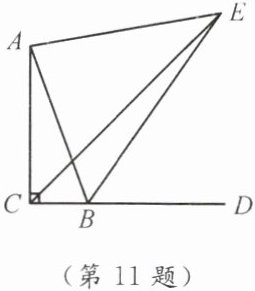
11. 如图,在 Rt△ABC 中,∠ACB= 90°,∠BAC= 20°,∠ACB 的平分线与外角∠ABD 的平分线交于点 E,连结 AE,则∠AEC= ______°。

35

答案： 35