《2025年新课标学习方法指导丛书八年级数学上册浙教版》

12. 如图,三个三角形分别为用6根、7根、8根等长的火柴首尾顺次相接搭成的。

(1)4根火柴首尾顺次相接不能搭成三角形。(填“能”或“不能”)
(2)9根、11根火柴首尾顺次相接能搭成几种不同的三角形？请分别写出它们的边长。
9根火柴能搭成3种不同的三角形，边长分别为(1,4,4)，(2,3,4)，(3,3,3)；11根火柴能搭成4种不同的三角形，边长分别为(1,5,5)，(2,4,5)，(3,3,5)，(3,4,4)。

答案：
(1)不能。
(2)
9根火柴：
设三角形三边长分别为$a$、$b$、$c$，$a + b + c = 9$，且$a + b＞c$，$a + c＞b$，$b + c＞a$。
当$a = 1$，$b = 4$，$c = 4$时，$1 + 4＞4$，$1+4 ＞ 4$，$4 + 4＞1$，可以构成三角形。
当$a = 2$，$b = 3$，$c = 4$时，$2 + 3＞4$，$2+4 ＞ 3$，$3 + 4＞2$，可以构成三角形。
当$a = 3$，$b = 3$，$c = 3$时，$3 + 3＞3$，可以构成三角形。
所以9根火柴能搭成3种不同的三角形，边长分别为$(1,4,4)$，$(2,3,4)$，$(3,3,3)$。
11根火柴：
设三角形三边长分别为$a$、$b$、$c$，$a + b + c = 11$，且$a + b＞c$，$a + c＞b$，$b + c＞a$。
当$a = 1$，$b = 5$，$c = 5$时，$1 + 5＞5$，$1+5 ＞ 5$，$5 + 5＞1$，可以构成三角形。
当$a = 2$，$b = 4$，$c = 5$时，$2 + 4＞5$，$2+5 ＞ 4$，$4 + 5＞2$，可以构成三角形。
当$a = 3$，$b = 3$，$c = 5$时，$3 + 3＞5$，$3+5 ＞ 3$，$3 + 5＞3$，可以构成三角形。
当$a = 3$，$b = 4$，$c = 4$时，$3 + 4＞4$，$3+4 ＞ 4$，$4 + 4＞3$，可以构成三角形。
所以11根火柴能搭成4种不同的三角形，边长分别为$(1,5,5)$，$(2,4,5)$，$(3,3,5)$，$(3,4,4)$。

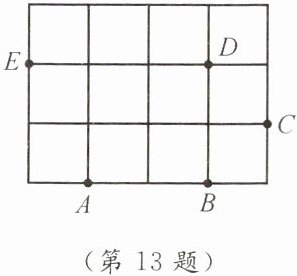
13. 如图,过A,B,C,D,E五点中任意三点画三角形,其中以AB为一边可以画出3个三角形,以点C为顶点可以画出5个三角形。

答案： 3,5

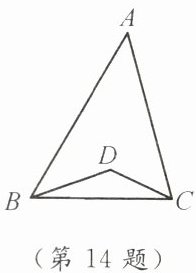
14. 如图,在△ABC中,∠DBC= $\frac{1}{3}$∠ABC,∠DCB= $\frac{1}{3}$∠ACB,∠A= 45°,则∠BDC= 135°。

答案： 135

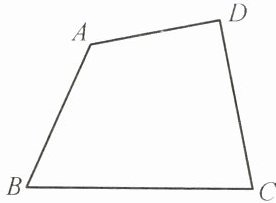
15. 如图,在四边形ABCD内找一点O,使OA+OB+OC+OD的值最小,并说出你的理由。

答案： 点$O$应取为四边形对角线$AC$与$BD$的交点。
理由：
根据两点之间线段最短，得
当点$O$为四边形对角线$AC$与$BD$的交点时，
$OA+OC$取得最小值，$OB+OD$取得最小值，
此时$OA + OB + OC + OD$的值最小。