第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
9. 如图,AC= AD,BC= BD,下列结论一定正确的是(
A.CD平分∠ACB
B.CD垂直平分AB
C.AB垂直平分CD
D.AB与CD互相垂直平分
C
)A.CD平分∠ACB
B.CD垂直平分AB
C.AB垂直平分CD
D.AB与CD互相垂直平分
答案:
C
10. 如图,三座商场分别坐落在A,B,C所在位置,现要规划一个地铁站,使得该地铁站到三座商场的距离相等,该地铁站应建在(
A.三角形三条中线的交点
B.三角形三条高所在直线的交点
C.三角形三个内角的平分线的交点
D.三角形三条边的垂直平分线的交点
D
)A.三角形三条中线的交点
B.三角形三条高所在直线的交点
C.三角形三个内角的平分线的交点
D.三角形三条边的垂直平分线的交点
答案:
D
11. 如图,在△ABC中,AB,AC的垂直平分线分别交BC于点D,E,垂足分别为M,N,已知△ADE的周长为22,则BC的长为
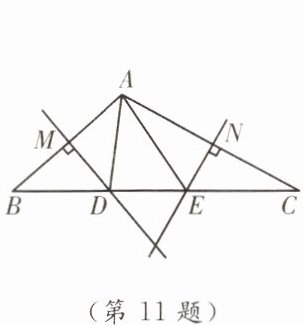
22
。
答案:
22
12. 如图,在△ABC中,∠A= 60°,P为△ABC内一点,过点P的直线EF分别交AB,AC于点E,F。若点E,F分别在PB,PC的垂直平分线上,则∠BPC的度数为
120°
。
答案:
120°
13. 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE= AC。
(1)求证:AD⊥BC。
(2)若∠B= 35°,求∠C的度数。
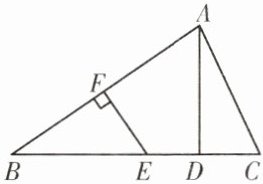
(1)求证:AD⊥BC。
(2)若∠B= 35°,求∠C的度数。

答案:
(1)证明:
连接$AE$。
$\because EF$是$AB$的垂直平分线,
$\therefore AE=BE$。
$\because BE=AC$,
$\therefore AE=AC$。
$\because D$为线段$CE$的中点,
$\therefore AD\perp BC$。
(2)解:
$\because AE=BE,\angle B=35^\circ$,
$\therefore \angle EAB=\angle B=35^\circ$,
$\therefore \angle AEC=\angle EAB+\angle B=70^\circ$。
$\because AE=AC$,
$\therefore \angle C=\angle AEC=70^\circ$。
连接$AE$。
$\because EF$是$AB$的垂直平分线,
$\therefore AE=BE$。
$\because BE=AC$,
$\therefore AE=AC$。
$\because D$为线段$CE$的中点,
$\therefore AD\perp BC$。
(2)解:
$\because AE=BE,\angle B=35^\circ$,
$\therefore \angle EAB=\angle B=35^\circ$,
$\therefore \angle AEC=\angle EAB+\angle B=70^\circ$。
$\because AE=AC$,
$\therefore \angle C=\angle AEC=70^\circ$。
查看更多完整答案,请扫码查看


