第3页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
【例1】三角形的两边长分别为3和5且周长为奇数,求这个三角形的周长。
【分析】要求三角形的周长,关键在于求得第三边的边长,因此根据三条线段能围成三角形的条件求得第三边的取值范围,从而可以求出第三边的长。
解:设第三边的长为x,根据三角形的三边关系,可知第三边的取值范围是5-3<x<5+3,即2<x<8。
又因为周长必须为奇数,所以第三边只能取3,5,7,那么周长可以是11,13,15。
【分析】要求三角形的周长,关键在于求得第三边的边长,因此根据三条线段能围成三角形的条件求得第三边的取值范围,从而可以求出第三边的长。
解:设第三边的长为x,根据三角形的三边关系,可知第三边的取值范围是5-3<x<5+3,即2<x<8。
又因为周长必须为奇数,所以第三边只能取3,5,7,那么周长可以是11,13,15。
答案:
设第三边的长为$x$。
根据三角形三边关系:$5 - 3 < x < 5 + 3$,即$2 < x < 8$。
已知两边长为$3$和$5$,周长为奇数,两边之和为$3 + 5 = 8$(偶数),则第三边$x$需为奇数(偶数 + 奇数 = 奇数)。
在$2 < x < 8$范围内的奇数有$3$,$5$,$7$。
当$x = 3$时,周长为$3 + 5 + 3 = 11$;
当$x = 5$时,周长为$3 + 5 + 5 = 13$;
当$x = 7$时,周长为$3 + 5 + 7 = 15$。
答:这个三角形的周长为$11$或$13$或$15$。
根据三角形三边关系:$5 - 3 < x < 5 + 3$,即$2 < x < 8$。
已知两边长为$3$和$5$,周长为奇数,两边之和为$3 + 5 = 8$(偶数),则第三边$x$需为奇数(偶数 + 奇数 = 奇数)。
在$2 < x < 8$范围内的奇数有$3$,$5$,$7$。
当$x = 3$时,周长为$3 + 5 + 3 = 11$;
当$x = 5$时,周长为$3 + 5 + 5 = 13$;
当$x = 7$时,周长为$3 + 5 + 7 = 15$。
答:这个三角形的周长为$11$或$13$或$15$。
【例2】下列语句中哪些是命题?
①单位面积所受的压力叫作压强。
②如果a是实数,那么$a^2+1>0。$
③两个无理数的乘积一定是无理数。
④偶数一定是合数吗?
⑤连结AB。
⑥不相等的两个角不可能是对顶角。
【分析】一般地,判断某一件事情的句子叫作命题。如果是以祈使句或疑问句的形式出现的句子肯定不是命题。特别要注意,如果是作出错误判断的句子,也是命题。
解:命题是①②③⑥。
①单位面积所受的压力叫作压强。
②如果a是实数,那么$a^2+1>0。$
③两个无理数的乘积一定是无理数。
④偶数一定是合数吗?
⑤连结AB。
⑥不相等的两个角不可能是对顶角。
【分析】一般地,判断某一件事情的句子叫作命题。如果是以祈使句或疑问句的形式出现的句子肯定不是命题。特别要注意,如果是作出错误判断的句子,也是命题。
解:命题是①②③⑥。
答案:
①是命题,因为它是一个定义,判断了“单位面积所受的压力叫作压强”这一事情。
②是命题,因为它是一个可以判断真假的陈述句,对于所有实数$a$,$a^2+1>0$总是成立的。
③是命题,因为它是一个可以判断真假的陈述句,但需要注意的是,这个命题是假的,例如$\sqrt{2} × \sqrt{2} = 2$是一个有理数。
④不是命题,因为它是一个疑问句,不能作出判断。
⑤不是命题,因为它是一个祈使句,不能作出判断。
⑥是命题,因为它是一个可以判断真假的陈述句,不相等的两个角确实不可能是对顶角。
所以命题是①②③⑥。
②是命题,因为它是一个可以判断真假的陈述句,对于所有实数$a$,$a^2+1>0$总是成立的。
③是命题,因为它是一个可以判断真假的陈述句,但需要注意的是,这个命题是假的,例如$\sqrt{2} × \sqrt{2} = 2$是一个有理数。
④不是命题,因为它是一个疑问句,不能作出判断。
⑤不是命题,因为它是一个祈使句,不能作出判断。
⑥是命题,因为它是一个可以判断真假的陈述句,不相等的两个角确实不可能是对顶角。
所以命题是①②③⑥。
【例3】如图,试说明∠A+∠ABC+∠C= ∠ADC。
【分析】四边形中的问题往往转化为三角形来解决。本题通过添加辅助线,利用三角形的一个外角等于与它不相邻的两个内角的和来说明。
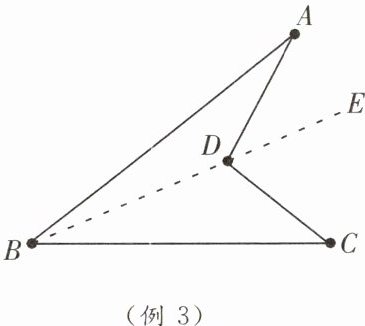
解:如图,连结BD并延长至点E。
在△ABD中,∠ADE= ∠ABD+∠A,
在△BCD中,∠CDE= ∠CBD+∠C。
又因为∠ADC= ∠ADE+∠CDE,
所以∠ADC= ∠ABD+∠A+∠CBD+∠C= ∠A+∠ABC+∠C。
【分析】四边形中的问题往往转化为三角形来解决。本题通过添加辅助线,利用三角形的一个外角等于与它不相邻的两个内角的和来说明。

解:如图,连结BD并延长至点E。
在△ABD中,∠ADE= ∠ABD+∠A,
在△BCD中,∠CDE= ∠CBD+∠C。
又因为∠ADC= ∠ADE+∠CDE,
所以∠ADC= ∠ABD+∠A+∠CBD+∠C= ∠A+∠ABC+∠C。
答案:
连结BD并延长至点E。
在△ABD中,∠ADE = ∠ABD + ∠A。
在△BCD中,∠CDE = ∠CBD + ∠C。
因为∠ADC = ∠ADE + ∠CDE,
所以∠ADC = ∠ABD + ∠A + ∠CBD + ∠C = ∠A + ∠ABC + ∠C。
在△ABD中,∠ADE = ∠ABD + ∠A。
在△BCD中,∠CDE = ∠CBD + ∠C。
因为∠ADC = ∠ADE + ∠CDE,
所以∠ADC = ∠ABD + ∠A + ∠CBD + ∠C = ∠A + ∠ABC + ∠C。
查看更多完整答案,请扫码查看


