《2025年新课标学习方法指导丛书八年级数学上册浙教版》

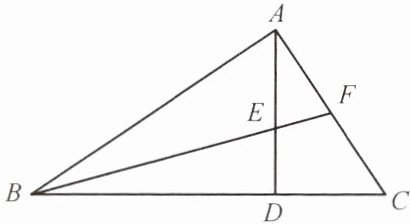
7. 如图,在△ABC中,∠BAC= 90°,AD⊥BC于点D,AD与∠ABC的平分线BF交于点E。求证：△AEF是等腰三角形。
]

答案： 证明：
∵∠BAC=90°，AD⊥BC，
∴∠ADB=90°，∠BAD+∠ABD=90°，∠C+∠ABD=90°，
∴∠BAD=∠C（同角的余角相等）。
∵BF平分∠ABC，
∴∠ABF=∠CBF（角平分线定义）。
设∠ABF=∠CBF=α，则∠ABC=2α，∠C=90°-2α，∠BAD=∠C=90°-2α。
在△ABF中，∠BAC=90°，
∴∠AFB=180°-∠BAC-∠ABF=180°-90°-α=90°-α（三角形内角和定理）。
在△BDE中，∠ADB=90°，
∴∠DEB=180°-∠ADB-∠CBF=180°-90°-α=90°-α（三角形内角和定理）。
∵∠AEF=∠DEB（对顶角相等），
∴∠AEF=90°-α。
∴∠AFB=∠AEF（等量代换），即∠AFE=∠AEF。
∴AE=AF（等角对等边）。
∴△AEF是等腰三角形。

8. 给出下列三角形：①有两个角等于60°的三角形。②有一个角等于60°的等腰三角形。③三个外角(每个顶点处各取一个外角)都相等的三角形。④一腰上的中线也是这条腰上的高的等腰三角形。其中是等边三角形的有(D)
A.①②③
B.①②④
C.①③
D.①②③④

答案： D

9. 如图,在△ABC中,OB,OC分别是∠ABC和∠ACB的平分线,过点O作EF//BC,交AB,AC于点E,F,如果AB= 10,AC= 8,那么△AEF的周长为18。

答案： 18

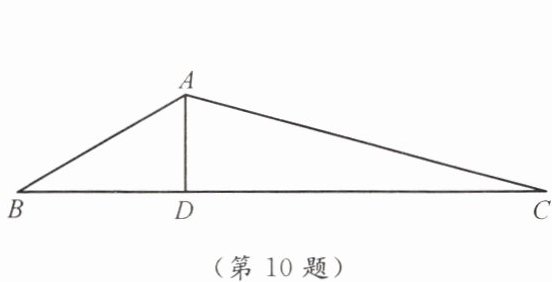
10. 如图,在△ABC中,∠BAC= 135°,AD⊥BC于点D,且AB+BD= DC,那么∠C= ______°。

15

答案： 15

11. 如图,D是△ABC中BC边上一点,AB= AC= BD,则∠1和∠2的关系是3∠1 - ∠2 = 180°。

答案： 3∠1 - ∠2 = 180°

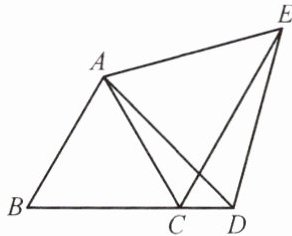
12. 如图,△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE= BD。求证：△ADE为等边三角形。
]

答案：
∵△ABC为等边三角形，
∴AB=AC，∠BAC=∠ABC=∠ACB=60°，BC=AC。
∵D为BC延长线上一点，
∴∠ACD=180°-∠ACB=120°。
∵CE平分∠ACD，
∴∠ACE=∠ECD=∠ACD/2=60°。
∵∠ABC=60°，D在BC延长线上，
∴∠ABD=∠ABC=60°，故∠ABD=∠ACE=60°。
在△ABD和△ACE中，
AB=AC，∠ABD=∠ACE，BD=CE，
∴△ABD≌△ACE（SAS）。
∴AD=AE，∠BAD=∠CAE。
∵∠BAC=∠BAD-∠CAD=60°，
又∠CAE=∠DAE+∠CAD，且∠BAD=∠CAE，
∴∠BAD-∠CAD=∠CAE-∠CAD，即∠BAC=∠DAE=60°。
∵AD=AE，∠DAE=60°，
∴△ADE为等边三角形。