《2025年新课标学习方法指导丛书八年级数学上册浙教版》

6. 将一直角三角尺与两边平行的纸条按如图所示的方式放置,有下列结论:①∠1= ∠2。②∠3= ∠4。③∠2+∠4= 90°。④∠4+∠5= 180°。其中正确的结论有(D)
A.1个
B.2个
C.3个
D.4个

答案： D

7. A,B,C,D,E五名同学猜测自己的数学成绩。
A说:"如果我得优,那么B也得优。"
B说:"如果我得优,那么C也得优。"
C说:"如果我得优,那么D也得优。"
D说:"如果我得优,那么E也得优。"
大家都没说错。如果A得优,那么他们之中有5人得优。

答案： 5

8. 已知∠A= (x-20)°,∠B= (80-3x)°,若∠A,∠B的两边分别平行且方向相同,则x= 25。

答案： 25

9. 如图,AB//DE,∠1= ∠ACB,∠BAC= $\frac{1}{2}$∠BAD。求证:AD//BC。

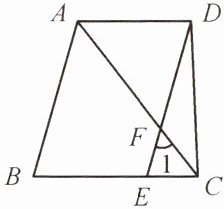
答案： 证明：
∵∠BAC=1/2∠BAD（已知），
∴∠BAC=∠CAD（角的和差定义）。
∵AB//DE（已知），
∴∠BAC=∠AFE（两直线平行，内错角相等）。
∵∠AFE=∠1（对顶角相等），
∴∠BAC=∠1（等量代换）。
∵∠1=∠ACB（已知），
∴∠BAC=∠ACB（等量代换）。
∴∠CAD=∠ACB（等量代换）。
∴AD//BC（内错角相等，两直线平行）。

10. 如图,已知直线c和a,b分别交于A,B两点,点P在直线c上运动。
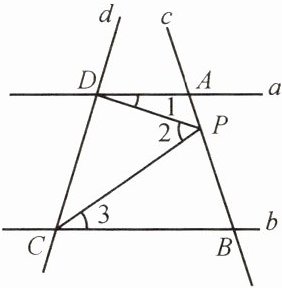
(1)若点P在A,B两点之间运动,试探究:当∠1,∠2和∠3之间满足什么数量关系时,a//b?
(2)若点P在A,B两点外侧运动,试探究:当∠1,∠2和∠3之间满足什么数量关系时,a//b?(直接写出结论即可)

答案：
(1) 当$\angle 1 + \angle 3 = \angle 2$时，$a // b$。
证明：
过点$P$作$PE// a$。
因为$\angle 1 = \angle DPE$（两直线平行，内错角相等）。
$\angle 2 = \angle DPE + \angle EPC$（角的和）。
因为$\angle 1 + \angle 3 = \angle 2$，所以$\angle 3 = \angle EPC$。
所以$PE// b$（内错角相等，两直线平行）。
因为$PE// a$，所以$a// b$（平行于同一条直线的两直线平行）。
(2) 当点$P$在$A$点外侧运动时，若$\angle 3 - \angle 1 = \angle 2$，则$a // b$；
当点$P$在$B$点外侧运动时，若$\angle 1 - \angle 3 = \angle 2$，则$a // b$。